Risk-to-Reward Ratio

A reward is always commensurate with risk in finance. If you want nearly zero risk, you must accept very low rates of return. The conventional “risk-free” asset is a government bond of a country that has a strong ability and willingness to avoid default, like the UK and the USA (but not excluding many others, such as Japan, Germany, Australia, et al.). But today, the US sovereign 10-year note yields about 2%, which is a mere 0.3% after inflation. Junk bonds yield more, but the name “junk” has real meaning — the risk of default and, therefore, of loss is far higher, varying from 3% to 40%. The risk-reward ratio in a good sovereign note is 1.03:1, although bond managers never think of it that way.

Low rates of return on safe assets are the primary reason that many traders prefer Forex. Given the high leverage available, you may be able to achieve rates of return of well over 10% and as high as 50% or more, at least sometimes. However, do not delude yourself — the risk you are taking to get extraordinary returns is itself extraordinary. That is because active trading in Forex has no pre-set rate of return like a note or bond or even an average historical rate of return as in equities.

You will be determining your rate of return based on the trading style and regime that you use and your money management skills. Since we have no external source to tell us what the rate of return should be, the starting point is the risk-reward numbers for your own trading strategy or system. Many analysts claim to have a 5:1 risk-reward ratio. This is quite improbable except for short periods of time. A more likely ratio over a long period of time is 3:1 or 2:1. Here is how risk-reward ratios work: if you have a reward that is three times the risk, meaning you make $3 for every $1 losing trade, and you make 25 trades of an equal amount per trade, you can lose on 18 trades or 72% of total trades and still do better than break even. If you have a 2:1 risk-reward ratio, you can have winners on only 9 trades of 25 (or 36% of total trades) to still be a little ahead. (You can test this out in an Excel spreadsheet if you like.)

This is why trading gurus always warn newcomers to accept that a system can have more losing trades than winning ones and still be successful. Arithmetically, this is no doubt correct — psychologically, it can be hard to live with a majority of trades being losers.

The arithmetic of the gain-loss ratio is also why trading advisors often say that seeking the “holy grail” of indicators or set-ups is not the right goal. The real holy grail is a thorough understanding of the gain-loss ratio. When you do understand its inexorable logic, you will be less inclined to trade impulsively or to meddle in your trading system and to override the very indicators that gave you the confidence to trade in the first place.

Gain-Loss Ratio

Technically, the gain-loss ratio is the actual booked gains and losses. If you made $1,000 and lost $500 over some specific period, your gain-loss ratio is 2:1. The risk-reward ratio is somewhat different — it is the amount you are willing to lose (say $500) in order to gain $1,000. Your risk-reward ratio is still 2:1.

In other words, most people consider that the gain-loss ratio is, in Forex, the equivalent of risk-reward. This is not strictly accurate. To see the difference, first, you need to know your gain-loss ratio in detail. Not what it should be, but what it is. Sit down and add up every winning trade and every losing trade over the past several months. If you have not started trading yet, you need to do this exercise by applying your system to past data to get hypothetical data. Divide the winners by the losers to get your win/loss ratio. Let’s say your trading generates a win/loss ratio of 2:1, meaning a $2 gain for every $1 lost.

This sounds pretty good, but it does not go far enough. The win/loss ratio does not link the gains and losses to the amount of capital you put at risk and does not help you figure out the expectancy for the next trade. Maybe you made one trade in the year that netted $200 on a capital stake of $10,000 and one that lost $100 in the same year on the same $10,000. You still have a 2:1 win-loss ratio, but the rate of return on capital is tiny. From these two trades, you cannot deduce a relevant risk-reward ratio, either. It looks like 2:1, but what was the capital amount you could have lost in each trade compared to the gain? If you had 5 trades and made $40 on each trade in the winning case, you would need to know the stop-loss amount to calculate the true risk-reward ratio. If it was, in fact, $20 per trade, then the risk-reward was indeed 2:1.

Expectancy

A sane and reasonable trading plan entails having a positive expectancy for every trade you take. This means you have a good reason to believe the trade will be profitable — not a guess, not a hope, but a real reason. You get confidence in the profitability of a trade from reliance on your indicators or indicator system. If you are a beginner without a track record, you need to run a demo account for a few months (or a few hundred trades, however long that takes) in order to get the data. If you already have trading experience under your belt, you need to have kept good records of your existing trades. If you are testing a trading system, you need to keep track of wins and losses.

Here is the formula for expectancy:

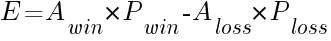
where:

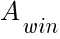— the average size of a profitable trade.

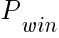— the percentage of winning trades among all trades.

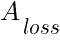— the average size of a losing trade.

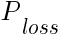— the percentage of losing trades among all trades.

Let’s say your trading, real or demo, or your indicator system would have generated this profile:

($800 × 35%) – ($400 × 65%) = $280 – $260 = $20

In other words, you hit a home run of $800 on 35% of the trades but big losses on a majority of trades, so your expected gain per trade on the next trade is a mere $20.

Here is a more realistic expectancy:

($400 × 55%) – ($200 × 45%) = $220 – $90 = $130

The expectancy formula above indicates 55% winning trades, and each gained $400, with 45% of total trades being losers but at a cost of $200 each. Using these indicators, your expectancy for the next trade is a net $130. This is a whole lot better than $20, but $130 on how much capital and over how many trades?

Capital Stake

If you are trading only four times per year, you might have a high probability of making 4 x $130 = $520, but if you are doing it on $10,000 starting capital, it does not make much sense to tie up such a large sum of money on only four trades. The right question here is how much money you want to make as a multiple of starting capital.

Capital Goal = Starting Capital + (Expectancy × Total Number of Trades)

Let’s say you have $10,000 to put into Forex trading, and you want to double it over a year to $20,000. Here is how to manage the arithmetic:

$20,000 = Starting Capital + ($130 × Number of Trades)

If you traded the full amount of $10,000 on every trade (and the expectancy remains stable at $130 per trade), you would have to make 76.9 trades per year to double your money:

$20,010 = $10,000 + ($130 × 77)

The problem here is that the number of trades per year is largely dictated by the system you select. Most indicators have built-in buy/sell signals, and, in addition, you should have a stop-loss regime in place that exits trades when conditions turn against you. If you pick a system plus stop-loss regime that trades, say, 35 times per year, you can expect to make $4,550, not $10,000. To get to a $10,000 capital gain in one year, you have to pick a different set of indicators and a different stop, which now changes your expectancy, and you have to start over at the first step above.

By adopting a rational, systematic approach, you will not have unrealistic expectations. Drilling down to expected total capital gain on the basis of your trading system’s expectancy and trading frequency plus your starting capital stake is the sanest of all possible ways to manage risk and reward.

Stops Are Central

You cannot control how far a move will go, which means your expected gain per trade can always fall short. But you can control the other side, how much you can lose. Stops are the tool for this. Stops can become tricky when you see or calculate a natural price level at which to place a stop, like the previous high/low, support/resistance, or a Fibonacci number. Unfortunately, these “natural” stop locations can fall at the level that would mean a very low position size (inconsistent with what your broker allows), considering your risk-reward requirement. To a certain extent, this can be a good thing since we suspect some players of “stop-hunting” at these obvious levels. However, you should place the stop where you think the chart is telling you to place it and not at the best fit to your gain-loss ratio. It can be helpful to draw horizontal lines to see how far away your optimum stop is from the natural one. It will make you grind your teeth.