ارتدادات فيبوناتشي
يفخر المتداولون من مستخدمي التحليل الفني بأنهم يطبقون طرق علمية في مراقبة حركة الأسعار فضلاً عن استعارة مفاهيم رياضية من مختلف العلوم التطبيقية... ولكنهم برغم ذلك يقعون فريسة لخرافة من العصور الوسطى لم يثبت صحتها في أي وقت. وتلك واحدة من الأسرار الكبيرة في عالم التداول.
أعاد عالم الرياضيات الإيطالي ليوناردو بيسانو بيغولو، والذي عاش خلال الفترة ما بين 1170 إلى 1250 في إيطاليا وكان يطلق عليه "فيبوناتشي" ("ابن بوناتشي") اكتشاف متوالية رقمية كانت معروفة في الهند قبل مولده بقرون عديدة. متوالية أو متسلسلة فيبوناتشي هي واحدة من بين عدد كبير من المتواليات الحسابية وإن كانت تتمتع ببعض الخصائص الفريدة. أحد الجوانب المثيرة للاهتمام في متوالية فيبوناتشي هو ارتباطها بالعديد من الظواهر الطبيعية مثل حلزون قوقعة نوتيلوس، بتلات عباد الشمس والعديد غيرها. من بين الخصائص الأخرى لمتوالية فيبوناتشي هو أنها تنطبق على الأرقام السالبة تماماً مثل الأرقام الموجبة. أيضاً فإن كل رقم ثالث هو إحدى مضاعفات 2، وكل رقم رابع هو مضاعف 3، بينما يمثل كل رقم خامس إحدى مضاعفات 4 وهلم جرا.
متوالية فيبوناتشي هي 0، 1، 1، 2، 3، 5، 8، 13، 21، 34، 55، 89، 144، الخ. يمثل كل رقم مجموع الرقمين السابقين. يكمن الجانب السحري في متوالية فيبوناتشي هو أن كل رقم يزيد عن الرقم الذي يسبقه بنسبة 1.618 تقريباً. تشكل هذه النسبة أساس المثلث السحري الذي استخدمه الإغريق القدماء في بناياتهم وأيضاً الرسامين على مر التاريخ في تحديد حجم اللوحات الأكثر راحة بالنسبة للعين البشرية. إذا قسمت أي رقم على الرقم الذي يسبقه ستحصل على النسبة 61.8%. قد تختلف الأرقام بعد الفاصلة العشرية بعض الشيء حيث قد لا تساوى 61.8% بالضبط. على سبيل المثال، 8 / 13 = 0.6153 و55 / 89 = 0.6179. كلما تحركت إلى أعلى مع سلسلة فيبوناتشي ستحصل على الرقم 1.618 أو 61.8. إحدى النسب الثابتة الأخرى التي تصاحب متوالية فيبوناتشي وتنطبق على جميع أرقامها هي 38.2% والتي نحصل عليها عن طريق قسمة أي رقم على الرقم الذي يليه في الترتيب بثلاثة خانات.
تُستخدم أرقام فيبوناتشي عادةً في عالم التداول لتقدير مقدار ارتداد حركة السعر قبل استئناف الاتجاه الأصلي. نعلم جميعاً أن الأسعار لا تتحرك في خط مستقيم بل في أشكال أقرب إلى الزجزاج حيث تأخذ خطوتين إلى الأمام وخطوة إلى الخلف. نستخدم نسب فيبوناتشي في قياس الخطوة إلى الخلف باعتبارها دالة في الخطوتين إلى الأمام. وتنصرف هذه العملية إلى إيجاد قاع ثم القمة التالية قبل الارتداد. نفترض أن هذا الارتداد أو التصحيح سيصل إلى إحدى نسب فيبوناتشي الرئيسية – 23.6%، 38.2% أو 61.8%. عندما يرتد السعر حتى يصل إلى حدود المستوى 61.8% من الحركة الصعودية السابقة، عندها نتوقع أن يجد الدعم ويتوقف عن الهبوط. إذا لم يحدث ذلك، عندها تذهب توقعاتنا إلى استمرار الانخفاض وصولاً إلى أدنى قاع أي النقطة التي بدأت منها الحركة الصعودية والتي تمثل أيضاً نسبة الارتداد 100% (وذلك برغم أن الرقم 100 ليس ضمن متوالية فيبوناتشي). يقوم معظم المحللين أيضاً بإدخال مستوى الارتداد 50% وهي فكرة طبقها واحد من أشهر المتداولين في بدايات القرن العشرين وهو وليام جان ، وذلك برغم أن الرقم 50% لا يندرج أيضاً ضمن متوالية فيبوناتشي.
انظر إلى الرسم البياني أدناه والذي يظهر تطبيق مثالي لارتدادات فيبوناتشي حيث ارتد زوج GBP/USD إلى حدود المستوى 61.8% بعد حركة صعودية قوية. يبدو هذا الرسم البياني مثالياً للادعاء بجدوى تطبيق متوالية فيبوناتشي.
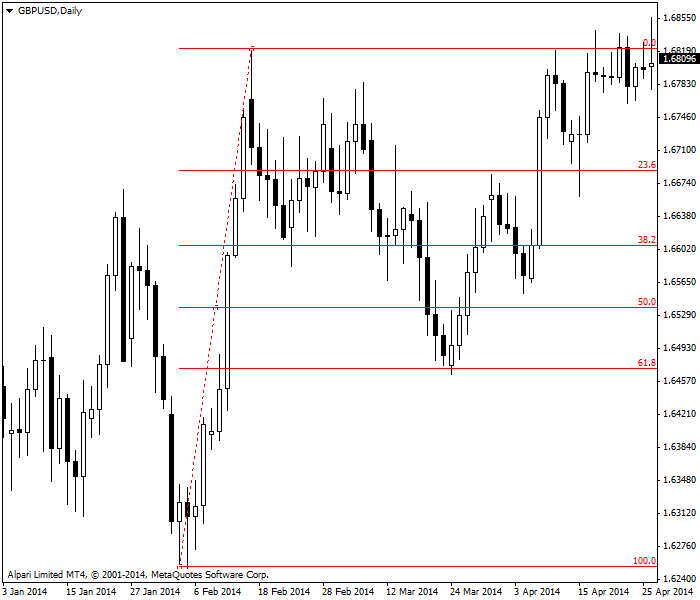
قارن الآن هذا الوضع مع الرسم البياني التالي حيث كسر السعر حاجز 61.8% فيبوناتشي. ارتد السعر بعد ذلك إلا أنه عاد في نهاية المطاف إلى حاجز التصحيح 100% قبل أن يرتد صعوداً ليتجاوز أعلى قمة سابقة. ربما نقول أن وضع الدعم عند مستوى الارتداد 61.8% كانت فكرة فاشلة إلا أنها "نظرياً" برهنت على فائدتها في نهاية المطاف حيث وصل السعر إلى المستوى 100% تقريباً بعد كسر حاجز الارتداد 61.8%.
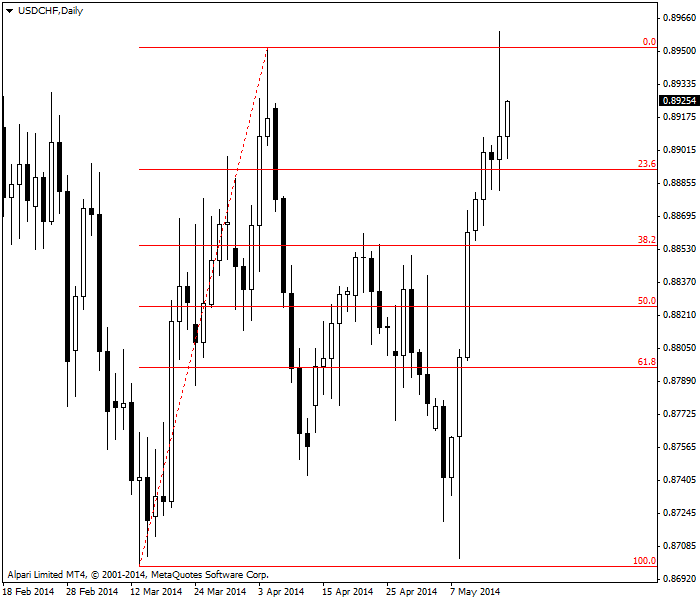
يظهر الشكل التالي زوج EUR/USD على إطار الأربع ساعات. من الواضح أن المكان المثالي لوضع أمر إيقاف لصفقة بيع على اليورو كان أعلى مستوى الارتداد 25%.
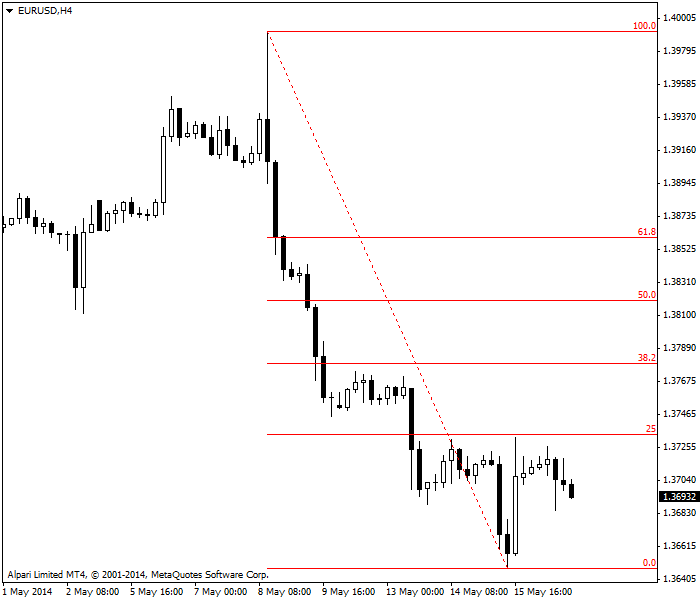
يظهر المثال أدناه إطار 5 دقائق لزوج EUR/USD . تجاوزت الحركة التصحيحية مستوى 50% إلا أنها لم تتمادى لكسر 61.8% وهو ما استنتجنا منه ضعف الحركة الصعودية وبالتالي قررنا الدخول في صفقة بيع. وكما يبدو واضحاً واصل السعر هبوطه حتى الوصول إلى أدنى قاع على الرسم البياني والذي يمثل نقطة بداية الحركة التصحيحية قبل أن يستأنف التحرك صعوداً مرة أخرى. وكقاعدة عامة، تعطي ارتدادات فيبوناتشي نتائج أفضل على الأطر الزمنية القصيرة مقارنة بإطار اليومي أو الأسبوعي وهو ما قد يعزى إلى أن العديد من متداولي المدى القصير يتبنون مفهوم ارتدادات فيبوناتشي.
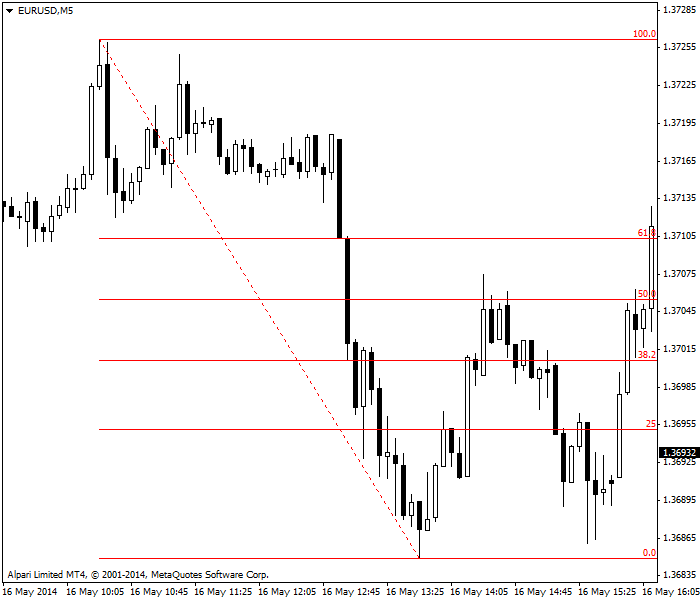
لا يوجد سبب مقنع لتفسير حركة أسعار الأوراق المالية وفقاً لمتوالية فيبوناتشي بشكل يختلف عن احتمالات تتبع السعر لأي متوالية هندسية أو رقمية أخرى، أو حتى وفق الرقم الذهبي الإغريقي pi. جميع المتواليات الرقمية تندرج تحت وصف "القوانين الطبيعية" – وليست لها ميزة تتفوق بها عن أي أرقام ذهبية مثل pi. كما لا يوجد أي تفسير علمي أو منطقي يبرر السبب في أن أسعار الأوراق المالية، بما في ذلك العملات، سوف تتحرك وفقاً لمتسلسلة فيبوناتشي. التفسير المنطقي الوحيد هو أنه:
- لوحظ في عدد كافي من الحالات أن الأسعار تبدو وكأنها تتبع أرقام المتوالية
- يعتقد عدد كبير من المتداولين أن متوالية فيبوناتشي ستحقق نتائج جيدة وبالتالي يقومون بتطبيقها وهو ما يجعلها أقرب إلى – النبوءة التي تحقق نفسها بنفسها.
هناك إيمان قوي بفاعلية متوالية فيبوناتشي في سوق الفوركس وذلك برغم عدم وجود دراسات أكاديمية محترمة تبرهن على فرضية أن أسعار الفوركس تتبع متوالية فيبوناتشي. ولكن لأن العديد من متداولي الفوركس يتبنى هذا المفهوم فلم تعد هناك أهمية للبحث عن أدلة لتبرير هذا السلوك. رسم خطوط فيبوناتشي أصبح بالنسبة للعديد من المتداولين أقرب إلى المهام الروتينية التي يقومون بها دون تفكير.