خطر الخراب

أحد الأمور التي تشغل بال أي متداول في الفوركس هو معرفة مدى خطورة الاستراتيجية التي يستخدمها وما هي فرص خسارة جزء من رصيد الحساب أو الرصيد بأكمله. يطلق على هذا الاحتمال خطر الإفلاس أو خطر الخراب أو خطر الدمار الشامل. وبما أن متداولي الفوركس يكونوا على دراية عادةً بنسبة النجاح/الفشل ومتوسط حجم الصفقات الرابحة والخاسرة، فإن حساب خطر الإفلاس من المفترض أن يكون سهلاً نسبيًا. أليس كذلك؟ لسوء الحظ، الأمر ليس بهذه البساطة.

خطر الإفلاس هو مشكلة معروفة في نظرية الاحتمالات، ويمكن حلها إلى حد ما باستخدام قوانين ومعادلات هذه النظرية. يعد تقييم مخاطر الإفلاس في الفوركس مهمة معقدة للغاية تتطلب الكثير من البحث والعمليات الحسابية حتى يتسنى الوصول إلى مستوى مقبول من الدقة.

إحدى الطرق الأكثر شيوعًا لحساب مخاطر الإفلاس هي استراتيجية الفوركس التي تنطوي على معادلتين ثابتتين لحساب حجم المركز الثابت و تحديد حجم المركز وفق نسبة ثابتة وهي طريقة تستخدمها بالفعل العديد من شبكات التداول الاجتماعي للفوركس (مثل FXSTAT, Myfxbook، والعديد غيرها). قدم هذه الاستراتيجية D.R. Cox و H.D. Miller في نظرية العمليات العشوائية وهي متاحة للجمهور من مصادر مختلفة (على سبيل المثال تقليل خطر الإفلاس بقلم ديفيد إي شامنس في عدد أغسطس 2009 من مجلة Futures Magazine). وبرغم أن العملية تبدو معقدة للغاية للوهلة الأولى، ولكن يمكنك إجراء هذه الحسابات باستخدام آلة حاسبة أو جدول بيانات إكسل.

خطر الإفلاس مع حجم مركز التداول الثابت

تشير حالة ’حجم مركز التداول الثابت‘ إلى أن المتداول لن يقوم بزيادة أو تقليل حجم الصفقة سواء حققت صفقاته الجديدة مكاسب أو خسائر. على سبيل المثال، إذا بدأ المتداول برصيد حساب 10,000$ و1 لوت قياسي لكل مركز، ثم انخفض رصيد الحساب إلى 1,000$ أو تضاعف إلى 50,000$، فإن هذا لن يغير من حجم مركز التداول البالغ 1 لوت. يتناسب احتمال خسارة جزء من الرصيد مع الانحراف المعياري للحساب ويتناسب عكسيًا مع حجم هذا الجزء ومتوسط العائد لكل صفقة. ستأخذ معادلة خطر الإفلاس الصيغة التالية:

حيث:

• e هو رقم أويلر (~2.71828),
• A هو متوسط نسبة العائد لكل صفقة (على سبيل المثال، إذا حققت صفقاتك عائد بنسبة 2% من رصيد الحساب في المتوسط، في هذه الحالة فإن A = 0.02)،
• Z هو الجزء من الحساب الذي تقوم بتقييم مخاطر خسارته (على سبيل المثال، لحساب مخاطر خسارة 40% من الحساب، Z = 0.4),
• D هو الانحراف المعياري لعائدات صفقاتك (يجب حسابه في شكل نسبي وليس وحدات من العملة).

 

مثال 1:

خطر خسارة 10% من رصيد الحساب مع الأخذ في الاعتبار أن متوسط العائد 2% لكل صفقة وانحراف معياري بنسبة 7%.

مثال 2:

خطر الإفلاس الكامل (100% من رصيد الحساب)، مع الأخذ في الاعتبار متوسط عائد 1.5% لكل صفقة وانحراف معياري بنسبة 1%.

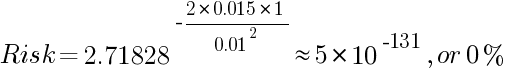
من السهل ملاحظة أن هذه المعادلة تحسب خطر الإفلاس لعدد لا نهائي من الصفقات. وفقًا لهذه المعادلة، ستكون مخاطر الخسارة دائمًا 100% للنظام الذي يُظهر في الوقت الحالي توقعًا سلبيًا لنتائج الصفقات وسيظل قريبًا بدرجة كافية (ولكن ليس مساويًا) للصفر بالنسبة لمتوسط العائد الكافي المرتفع والانحراف المعياري الكافي المنخفض للعائد.

المزايا:

1. تتسم هذه الطريقة بالبساطة الشديدة، حتى أنه يمكنك حساب المعادلة ذاتها باستخدام آلة حاسبة. الانحراف المعياري أكثر تعقيدًا بعض الشيء، ولكن لن يستغرق حسابه يدويًا بضع دقائق إذا كنت على دراية برصيد الحساب بعد كل صفقة. تستطيع إدخال تعليمات برمجية بسيطة داخل أي مؤشر أو اكسبيرت لحساب ذلك.
2. النتيجة دقيقة نوعًا ما.
3. يمكنك استخدامه لحساب مخاطر الخسارة لأي جزء من الحساب.

العيوب:

1. يستبدل "المخاطرة" الفعلية للصفقات بالانحراف المعياري، وهو أمر غير صحيح تمامًا.
2. يفترض ثبات معدل العائد الحالي والانحراف المعياري بمرور الوقت. الجمع بين معدل العائد الثابت وحجم المركز الثابت يكاد يكون مستحيلاً في الواقع العملي.
3. يفترض ثبات حجم مركز التداول رغم أن خسارة جزء من الرصيد قد يجبر متداول الفوركس على تقليل حجم صفقاته (على سبيل المثال، لن يكون بمقدور المتداول فتح مركز بحجم لوت قياسي إذا انخفض رصيد الحساب من 10,000$ إلى 800$).
4. يُظهر المخاطرة بعدد لا نهائي من الصفقات — لا أحد يتداول لهذه الفترة الطويلة باستخدام استراتيجية خاسرة.
5. الدقة ليست مثالية حتى إذا كانت جميع الافتراضات صحيحة في استراتيجية تداول معينة.

مخاطر الخسارة مع تحديد حجم المركز باستخدام نسبة ثابتة

على عكس نموذج حجم المركز الثابت، ينطوي تحديد حجم المركز وفق نسبة كسرية على قيام المتداول بالمخاطرة بجزء ثابت من حسابه في كل صفقة (على سبيل المثال، 1%) وبالتالي لا تهم هنا القيمة الفعلية أو المطلقة للصفقة. في هذه الحالة سيكون الربح تناسبي مع حجم الحساب فيما تتناسب معه الخسارة عكسيًا. وكما هو الحال مع حجم المركز الثابت، فإن احتمال خسارة جزء من الرصيد لا تزال تتناسب عكسيًا مع حجم هذا الجزء. لا يزال معامل اعتماد المخاطرة على الانحراف المعياري قيمة موجبة، بينما سيظل معامل الارتباط مع هذا الجزء سلبيًا، ولكن حسابه سيكون أكثر تعقيدًا. معادلة حساب المخاطر في هذه الحالة ستأخذ الصيغة التالية:

حيث:

• e هو رقم أويلر (~2.71828),
• A هو متوسط نسبة العائد لكل صفقة (على سبيل المثال، إذا كان عائد الصفقات 14% من رصيد الحساب في المتوسط، فإنA = 0.14),
• Z هو الجزء من الحساب الذي يجري تقييم مخاطر خسارته (على سبيل المثال، لحساب مخاطرة خسارة 25% من الحساب، Z = 0.25),
• D هو الانحراف المعياري لعائد الصفقات (يجب حسابه في صورة نسبة وليس وحدات من العملة).
• ln هو اللوغاريتمات الطبيعية.

فيما يلي مثالان على حساب خطر الإفلاس باستخدام نموذج تحديد حجم المركز باستخدام نسبة ثابتة مع تطبيق نفس الشروط المستخدمة في أمثلة حجم مركز التداول الثابت أعلاه:

 

مثال 1:

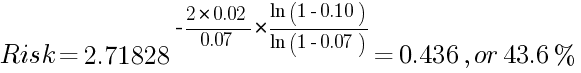
من الواضح أنها أقل بقليل من 44.2% من نموذج حجم المركز الثابت.

مثال 2:

نظرًا لأن استخدام جزء يعادل 100% من رصيد الحساب في المعادلة سيعني أن قيمة Z = 1، سيكون هناك خطأ في حساب اللوغاريتم الطبيعي (لم يتم تحديد الطبيعي عند 0، ولكنه رقم سالب كبير وغير محدود). هذا يعني أنه من المستحيل خسارة رصيد الحساب بالكامل إذا حققت الاستراتيجية معدل عائد إيجابي عند تطبيق نموذج تحديد حجم الصفقات باستخدام نسبة ثابتة:

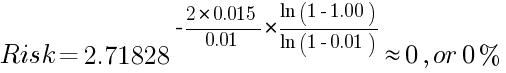
من الواضح أن هذه المعادلة تُظهر مخاطرة أقل لأنها تفترض نسبة كسرية في تحديد حجم مركز التداول، وهو ما يقلل حجم الصفقة في حالة تكبد خسارة، وبالتالي تقليل الخسائر الجديدة في الصفقات التالية.

المزايا:

1. تظل طريقة بسيطة للغاية في تقييم خطر الإفلاس. بالمقارنة مع معادلة حجم المركز الثابت، تمت إضافة بضع خطوات جديدة، ولكن تظل البيانات المستخدمة كما هي.
2. نحصل على نتيجة أكثر دقة عند تطبيقها في تحديد حجم مركز التداول.
3. يمكن استخدامها لحساب مخاطر خسارة أي جزء من الحساب أيضًا.

العيوب:

1. كما هو الحال مع معادلة حجم مركز التداول، يتم استبدال الخطر الحقيقي بالانحراف المعياري.
2. تفترض ثبات معدل العائد والانحراف المعياري.
3. تحسب المخاطرة لعدد غير محدود من الصفقات.

مشكلة إفلاس المقامر باستخدام سلاسل ماركوف

يتضح أن الطريقة الأكثر بداهة لحساب مخاطر الخسارة هي الأكثر صعوبة من حيث الحسابات الفعلية التي تنطوي عليها. يمكن تعريف مشكلة خطر الإفلاس في الفوركس بأنها حالة خاصة من مشكلة إفلاس المقامر، حيث يكون لدى المتداول (اللاعب)، والذي يبدأ برصيد حساب أولي (حصة)، احتمالية ربح متوسط مبلغ معين واحتمال مختلف (أو أحيانًا نفس الاحتمال) لخسارة مبلغ معين في المتوسط. يتنافس المتداول هنا ضد السوق (خصم ذات قدرات مالية غير محدودة) —، لهذا يمكن أن يخسر المتداول رصيد حسابه بالكامل: يمكن تعريف شرط النجاح بأنه الوصول إلى بعض التوازن المستهدف بحيث يكون الرصيد أعلى من مستواه الافتتاحي.

يمكنك الاطلاع على أبحاث عن المعادلات البسيطة لحساب مخاطر الخسارة باستخدام هذه الطريقة في الفصل 12 من مقدمة في الاحتمال والذي كتبه Charles M. Grinstead و J. Laurie Snell.

النجاح يساوي الخسارة، نفس الاحتمالات

إذا كان متوسط الربح مساويًا لمتوسط الخسارة، وكان احتمال الخسارة يعادل احتمال الفوز، فإن مهمة حساب خطر الإفلاس تصبح بسيطة للغاية. يشار إلى الرصيد الابتدائي بالرمز z والرصيد المستهدف M. وفي هذه الحالة سيكون خطر إفلاس الحساب قبل الانتقال منz إلى Mهي:

 

مثال 1:

الرصيد الافتتاحي هو 10,000$ (z). هناك احتمال بنسبة 50/50 لربح أو خسارة 1,000$ في كل صفقة. الرصيد المستهدف هو 20,000$ (M):

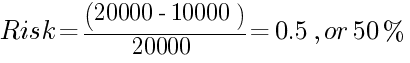
من الواضح أن احتمال ارتفاع الرصيد من 10,000$ إلى 20,000$ يعادل احتمال انخفاضه إلى 0$ هنا.

النجاح يساوي الخسارة، احتمالات مختلفة

احتمال النجاح (p) — هو احتمال نجاح صفقة واحدة (إنهاء على ربح). سيكون من المثير للاهتمام إذا كان المتداول يعرف بالضبط احتمال نجاحه في صفقة معينة، ولكن سنستخدم هنا نسبة النجاح/الفشل. يتم قسمة عدد الصفقات الرابحة على إجمالي عدد الصفقات وستكون النسبة الناتجة هي احتمال النجاح. لا توجد مشكلة في تضمين المراكز التي حققت أرباح صفرية، حيث سيتم تعويضها عن طريق احتساب متوسط حجم الربح، ولكن من الضروري تذكر القيام بعد هذه الصفقات قبل حسابها.

احتمال الخسارة (q) — هو احتمال خسارة مركز واحد (الإغلاق على خسارة). لنفس الأسباب المذكورة أعلاه، فإن نسبة النجاح/الفشل هي أفضل مقياس يمكن استخدامه هنا. q = عدد الصفقات الخاسرة على إجمالي عدد الصفقات. من الواضح أنه في حالة القيام بعد الصفقات ذات الأرباح الصفرية في عملية حساب p، فلن يتم تضمينها هنا.

إذا كان احتمال نجاح صفقة معينة لا يساوي احتمال خسارتها، فإننا سنضطر لاستخدام معادلة أكثر تعقيدًا. احتمال نجاح متوسط صفقة رابحة سيشار إليه بالرمز p، واحتمال خسارة الصفقة— q (p + q = 1). في هذه الحالة سيتم حساب خطر الإفلاس على النحو التالي:

 

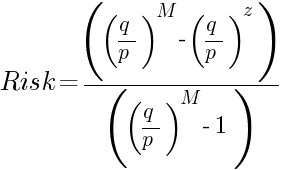
مثال 2:

الرصيد الافتتاحي كما هو — 10,000$(z)، أيضًا الرصيد المستهدف لن يتغير — 20,000$ (M)، ومتوسط الربح/الخسارة سيظل عند 1,000$ لكل صفقة، ولكن احتمال النجاح 0.55% واحتمال الفشل 0.45% (نظام تداول بميزة 5%). لتبسيط العمليات الحسابية، لا توجد مشكلة في قسمة الرصيد الافتتاحي والمستهدف على متوسط النجاح/الفشل للحصول علىz = 10 وM =20. يتم احتساب خطر الإفلاس قبل مضاعفة الرصيد على النحو التالي:

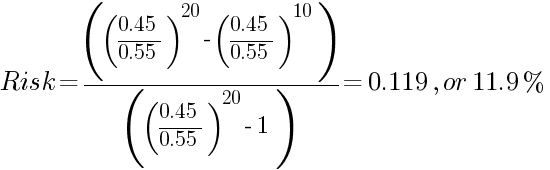
من الواضح أن ميزة الـ 5% تعطي متداول الفوركس أفضلية هائلة في موثوقية نظام التداول بأكمله.

حجم نجاح/فشل مختلف، احتمالات مختلفة

في الواقع العملي، من النادر أن تحقق استراتيجية تداول الفوركس متوسطات متساوية لربح وخسارة الصفقات. وبطبيعة الحال، فإن الاختلاف في نتائج الصفقات الرابحة والخاسرة يؤدي إلى زيادة تعقيد عملية حساب خطر الإفلاس. لا جدوى هنا من وضع الخوارزمية الكاملة لحساب الاحتمالات بالتفصيل في هذه الحالة. بدلاً من ذلك، من الأفضل إلقاء نظرة عامة على الخطوات الضرورية، والتي يمكن اختزالها بسهولة إلى مشكلات رياضية/برمجية بسيطة.

العمليات الحسابية

يمكن الاطلاع على معلومات تفصيلية حول العمليات الرياضية لحساب خطر الإفلاس للحالة العامة (احتمالات وحجم مختلف للربح/الخسارة) في مقالة كيفن براون إفلاس المقامر. قدم كيفن شرحًا رائعًا لهذه المشكلة وطرق حلها.

يمكن تصور عملية التداول باعتبارها حلقة مغلقة Markov model مع حالة افتتاحية واحدة (الرصيد الأولي، على سبيل المثال، 2,500$) و حالتان نهائيتان — 0$ ورصيدك المستهدف (على سبيل المثال، 5000$). هناك أيضًا عدد k من الحالات الانتقالية، والتي تعتمد على القاسم المشترك الأكبر (GCD) لمتوسط الربح ومتوسط الخسارة. على سبيل المثال، إذا كان متوسط الربح 1,000$ ومتوسط الخسارة 1,500$، فإن القاسم المشترك الأكبر أو GCD سيساوي 500$، وستكون هناك 9 حالات انتقالية (k = 9)، والتي تتضمن الحالة الافتتاحية. أخر حالتين انتقاليتين (4,000$ و4,500$) يرافقها احتمالp للوصول إلى الرصيد المستهدف، فيما الحالات الثلاثة الأولى (500$، 1,000$ و1,500$) سيرافقها الاحتمال q لإفلاس الحساب (الوصول إلى رصيد 0$).

بشكل عام، يمكن كتابة معادلة احتمال خسارة الحساب بأكمله قبل الوصول إلى الرصيد المستهدف على النحو التالي:

حيث:

• p احتمال نجاح صفقة.
• q احتمال خسارة صفقة.
• متجه الصف العلوي (a متجه خاسر) بطول عناصر k. متوسط الخسارة الأولى / GCD (خطوة الخسارة) هي q، بينما العناصر الأخرى 0.
• متجه الخط السفلي (a المتجه الكلي) هو أيضًا بطول k. عناصر متوسط الخسارة الأولى /GCD (خطوة الخسارة) هي q، متوسط الربح الأول / GCD (خطوة الربح) هيp، والباقي يساوي 0.
• M^-1 هي المصفوفة المعكوسة لمصفوفة المعاملM. M هو مصفوفة k×k التي بها 1 في جميع عناصرها القطرية الرئيسية. وبالإضافة إلى 1 من القطر، قد يحتوي كل عمود على ما يصل إلى عنصرين غير صفريين: -p — يتم وضعه أسفل القطر الرئيسي مع تساوي الإزاحة الرأسية منه إلى خطوة الربح; -q — يتم وضعه أسفل القطر الرئيسي مع إزاحة عمودية تساوي خطوة الخسارة.
• C_j هو مصفوفة من عمود واحد (متجه) بحجم k حيث تعادل جميع العناصر 0، باستثناء العنصر الموجود في الوضع j (حالة البداية)، والتي تعادل 1.

في المثال أعلاه، ستأخذ المصفوفة M الشكل التالي:

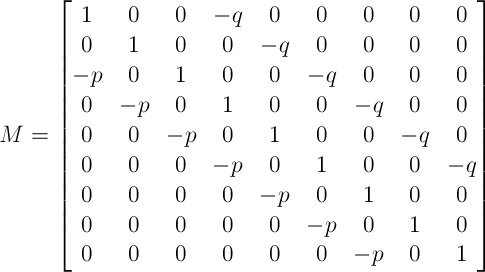
وإذا تم تعبئة القيم:

وسيتأخذ المتجه C_j الشكل التالي:

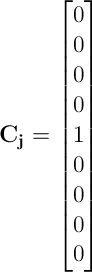
في حين أن ضرب المصفوفة/المتجه سيكون بديهيًا، فإن عكس مصفوفة أكبر من 3×3 لن يكون كذلك. أسهل طريقة للعثور على المصفوفة العكسيةM^-1 باستخدام جهاز كمبيوتر هو LU-decomposition. باستخدام المصفوفةL، من الممكن حل Ly = I لإيجاد y ثم استخدام المصفوفة U لحل Ux = y لإيجاد x، والتي ستكونM^-1. بعد ضرب المصفوفات الثلاثة للجزء العلوي والمصفوفات الثلاثة للجزء السفلي من المعادلة العامة سيصبح بعد ذلك هامشيًا.

التحسين

مثال الحالة هنا بسيط للغاية، المصفوفة هي 9×9 فقط — ويمكن حساب معكوسها بسرعة كبيرة دون الحاجة لإجراء أي تحسينات. ولكن ماذا لو كان GCD في الاستراتيجية يساوي 1$؟ على سبيل المثال، إذا كان متوسط الخسارة 1,113$ ومتوسط الربح 1,109$، و GCD يساوي 1$. مع رصيد افتتاحي 2,500$ ورصيد مستهدف 5,000$، فستكون لدينا مصفوفة بأبعاد 4,999×4,999 — سيستهلك ذلك قدر كبير من ذاكرة الكمبيوتر والوقت اللازم لإجراء العمليات الحسابية. أفضل وقت لحساب خطر الإفلاس بدون أي تحسينات هوO(k^2.376) وبشكل عام يتطلب ذاكرة k×k على الأقل.

أولاً، من المهم إبقاء مصفوفة M^-1 صغيرة قدر الإمكان. من الناحية المثالية، يجب أن يكون k أقل من 500، إذا كان الهدف هو حل المشكلة خلال وقت معقول (عدة ثواني).

يمكن تقليل الذاكرة المطلوبة بشكل كبير: يمكن تخزين المتجه الخاسر داخل المتجه الإجمالي (من المعروف أين يتوقف qفي المتجه الخاسر وبداية 0)، ويمكن تخزين نتائج تحليل LU داخل المصفوفة الرئيسية (M — يمكن تجاهله بعد التحليل).

ثالثًا، يمكن حل كلاً من Ly = I و Ux = y لعمود واحد (jth)، وذلك بدلاً من المصفوفةk×k بأكملها. سيكون نفس العمود أيضًا نتيجة الضرب في C_j. يعزى ذلك إلى أنه في حالة حساب المصفوفة k×k بأكملها ثم ضربها في C_j، فسيكون الناتج أيضًا عمودjمن المصفوفة فقط، لأن جميع الأصفار تتواجد في C_j.

أخيرًا، من الممكن حساب حاصل ضرب المتجه الخاسر في العمود j وناتج المتجه الإجمالي مع هذا العمود في وقت واحد، حيث ستكون تكرارات خطوة الخسارة الأولى هي نفسها أثناء هذه العمليات الحسابية، فيما لن تكون هناك حاجة لأي تكرارات أخرى في المتجه الخاسر.

التطبيق

فيما يلي مثال على رمز PHP يستخدم الخوارزمية المذكورة أعلاه لاستخلاص خطر الإفلاس للمثال السابق:

/*
  الرصيد الافتتاحي:      $2,500.00
  الرصيد المستهدف:        $5,000.00
  متوسط الصفقة الخاسرة:     $1,500.00
  متوسط الصفقة الرابحة: $1,000.00
  احتمال الخسارة:      30%
  احتمال النجاح:       70%
*/
 
// القاسم المشترك الأكبر = $500.
$begin_state = 5; // الرصيد الافتتاحي مقسومًا على القاسم المشترك الأكبر.
$N = 9; // عدد الحالات الانتقالية؛ K في المقالة.
$loss_step = 3; //حجم الخسارة مقسومًا على القاسم المشترك الأكبر.
$win_step = 2; // حجم الربح مقسومًا على القاسم المشترك الأكبر.
$q = 0.3; // احتمال الخسارة.
$p = 0.7; // احتمال النجاح.
 
// تعبئة متجه Cj.
for ($i = 0; $i < $N; $i++)
if ($i == $begin_state - 1) $unitary_vector[$i] = 1;
else $unitary_vector[$i] = 0;
 
// تنفيذ متجه الخسارة والمتجه الكلي. متجه الخسارة هو في الواقع جزء من المتجه الكلي.
for ($i = 0; $i < $N; $i++)
if (($i - $loss_step) < 0) $total_vector[$i] = $q;
else if (($i + $win_step) >= $N) $total_vector[$i] = $p;
else $total_vector[$i] = 0;
 
//تعبئة المصفوفة الرئيسية. 
for ($i = 0; $i < $N; $i++)
for ($j = 0; $j < $N; $j++)
// القطر الرئيسي هو دائمًا 1.
if ($i == $j) $a[$i][$j] = 1;
//العناصر أعلى القطر الرئيسي تتعلق بالخسارة. 
else if ($j == $i + $loss_step) $a[$i][$j] = -$q;
// العناصر أسفل القطر الرئيسي تتعلق بالربح.
else if ($j == $i - $win_step) $a[$i][$j] = -$p;
else $a[$i][$j] = 0;
 
//تحليل LU.
for ($i = 0; $i < $N; $i++)
{
for ($j = $i; $j < min($N, $i + $loss_step); $j++) // U
for ($k = 0; $k <= $i - 1; $k++)
$a[$i][$j] -= $a[$i][$k] * $a[$k][$j];
 
for ($j = $i + 1; $j <= min($i + $win_step, $N - 1); $j++) // L
{
for ($k = 0; $k <= $i - 1; $k++)
$a[$j][$i] -= $a[$j][$k] * $a[$k][$i];
$a[$j][$i] /= $a[$i][$i];
}
}
 
// حل  Ly = I لعمود واحد (متجه_أحادي) والذي يساوي Cj لمعادلة إفلاس المقامر.
// سيتم تخزين الناتج y أيضًا في متجه_أحادي.
// ابدأ من حالة_البداية لأن جميع قيم X قبل 1 في المتجه_الأحادي ستكون دائمًا 0.
for ($i = $begin_state; $i < $N; $i++)
{
$sum = 0;
for ($j = 0; $j <= $i - 1; $j++)
$sum -= $a[$i][$j] * $unitary_vector[$j];
 
$unitary_vector[$i] = $unitary_vector[$i] + $sum;
}
 
// حل UX = y لعمود واحد تم حسابه في Ly = I.
// سيتم تخزين الناتج x في متجه_ أحادي.
لـ  ($i = $N - 1; $i >= 0; $i--)
{
$sum = 0;
لـ ($j = $N - 1; $j > $i; $j--)
$sum -= $a[$i][$j] * $unitary_vector[$j];
 
$unitary_vector[$i] = ($unitary_vector[$i] + $sum) / $a[$i][$i];
}
 
// ضرب المتجه_الكلي والجزء الخاسر منه في المتجه_الأحادي الناتج.
$loss = 0;
$total = 0;
for ($i = 0; $i < $N; $i++)
{
$product = $total_vector[$i] * $unitary_vector[$i];
if (($i - $loss_step) < 0) $loss += $product;
$total += $product;
}
$probability = $loss / $total;
echo "الخسارة: $loss <br>";
echo "الإجمالي: $total <br>";
echo "الاحتمال:  $probability <br>";

سيكون الناتج:

الخسارة: 0.25755603952
الإجمالي: 1
الاحتمال: 0.25755603952

إذًا، سيكون احتمال خسارة الحساب بأكمله قبل مضاعفته تقريبًا 25.8% في هذا المثال.

ولكن ماذا لو أصبح k كبيرًا للغاية؟ في هذه الحالة، سيتم تطبيق التقريب الرياضي على خطوة الخسارة، خطوة الربح، والرصيدين الافتتاحي والمستهدف، وهو ما سيؤدي إلى اقتطاع كافة الأرقام الأخيرة تقريبًا. بالإضافة لذلك، يمكن أن يؤدي إلى تقليل الرصيد المستهدف. تؤثر الطريقة الأولى على الدقة، ولكن هذا التأثير يصبح أقل أهمية مع زيادة الفارق بين متوسط الخسارة ومتوسط الربح.

المزايا

1. إذا افترضنا أن بيانات الإدخال (الاحتمالات وحجم الربح/الخسارة) دقيقة بنسبة 100%، فإن هذه الطريقة ستقدم لنا نتائج دقيقة للغاية.
2. لا تعتمد على طريقة تحديد حجم مركز التداول، ولكن بالأحرى على متوسط الربح/الخسارة الناتجة بالأرقام المطلقة — وهي إحصائيات متاحة بسهولة في جميع تقارير استراتيجيات الفوركس.
3. معاملات الإدخال الأخرى بسيطة أيضًا للغاية — ليست هناك حاجة لحساب الانحراف المعياري.
4. يمكن حساب الحالات البسيطة يدويًا.
5. الخطر المحسوب هو "خسارة كل شيء قبل الوصول إلى الرصيد المستهدف" — وهو أمر يمكن تحقيقه على عكس نموذج "عدد الصفقات اللانهائي" في الطرق السابقة.

العيوب

1. افتراض أن المعلمات الرئيسية لاستراتيجية التداول (معدلات وأحجام الربح/الخسارة) لا تتغير. هذا الأمر ليس صحيحًا ولا منطقيًا في الواقع العملي.
2. طريقة معقدة للغاية.
3. تتطلب في بعض الحالات قدر كبير من القدرة الحاسوبية وعدد كبير من عمليات تقريب الأرقام، ما يقلل من دقة النتائج.

خطر الإفلاس باستخدام محاكاة مونت كارلو

محاكاة مونت كارلو ) يطلق عليها أيضًا طريقة مونت كارلو ) هي نموذج يتنبأ باحتمالات النتائج المختلفة التي تنطوي على متغيرات عشوائية. يعود الفضل في اختراع هذه الطريقة إلى عالم الرياضيات Stanislaw Ulam، وأطلق عليها لاحقًا مونت كارلو في إشارة إلى واحدة من أبرز مراكز المقامرة الشهيرة في موناكو. يبدو الاسم مناسبًا لأن المقامرة ترتبط عادةً بالصدفة والنتائج العشوائية.

ينطوي جوهر طريقة مونت كارلو على محاكاة النتائج عدة مرات باستخدام متغيرات عشوائية والحصول على قيم جديدة مع كل محاكاة. لفهم كيفية عمل هذه الطريقة بشكل أفضل، دعنا نلقي نظرة على أحد المواقف الافتراضية.

باستخدام البيانات التاريخية والاختبار الرجعي، لنفترض أنك قمت بحساب احتمالات الربح أو الخسارة لمتوسط الصفقة في استراتيجية التداول التي تستخدمها، جنبًا إلى جنب مع متوسط حجم الأرباح والخسائر. كيف تحسب خطر الإفلاس باستخدام هذه البيانات؟ يمكنك أيضًا محاولة محاكاة النتيجة عن طريق اختبار عشوائي لكل صفقة ومعرفة ما إذا كان رصيدك سيصبح صفر في نهاية المطاف. ولكن محاكاة واحدة لن تكون ذات فائدة كبيرة لأنها تُظهر نتيجة واحدة فقط من بين العديد من الاحتمالات دون أن تخبرك بدرجة احتمالية حدوثها.

ولكن ماذا لو قمت بمحاكاة النتيجة مائة مرة؟ أو ألف؟ أو عشرة ألاف؟ تشير طريقة مونت كارلو إلى أنه من خلال التوزيع العشوائي لنتيجة كل صفقة (الربح أو الخسارة، وربما حجم الربح أو الخسارة) ستحصل على بيانات إحصائية مفيدة عند إعادة تشغيل هذه المحاكاة. وكلما زاد عدد مرات المحاكاة التي تجريها، كلما زادت إمكانية الاعتماد على هذه البيانات. في حالة تداول الفوركس، سيساعد النظر إلى عدد المرات التي أدى فيها استخدام استراتيجية معينة إلى تصفير رصيد حسابك في تحديد خطر الإفلاس.

مثال على محاكاة مونت كارلو في جدول بيانات إكسل.

يُظهر جدول بيانات إكسل مثال بسيط على طريقة محاكاة مونت كارلو. يفترض هذا المثال أنك تعرف احتمال نجاح الصفقة وكذلك حجم متوسط الربح ومتوسط الخسارة.

أدخل حجم رصيد حسابك في خانة رصيد الحساب الافتتاحي. أدخل احتمال الربح في خانة احتمال النجاح كرقم يتراوح من 0 إلى 1. على سبيل المثال، إذا كان احتمال النجاح 65% عندها ينبغي إدخال القيمة في الحقل المشار إليه عند 0.65%. بعد ذلك، أدخل القيم في خانات متوسط الربح ومتوسط الخسارة في الحقول المقابلة. إذا كنت تفضل استخدام نطاق بدلاً من رقم متوسط ثابت، يمكنك القيام بذلك بسهولة من خلال الدالة RANDBETWEEN. في الخطوة التالية، قم بإدخال العدد المطلوب من صفقات المحاكاة وعدد مرات المحاكاة في خانات# of Trades و # of Simulations على التوالي. بعد تعبئة جميع الخانات المطلوبة يمكنك حساب خطر الخسارة. للقيام بذلك اذهب إلى Formulas في النافذة الرئيسية لملف إكسل وانقر على Calculate Now على يسارCalculation Options. أو بدلاً من ذلك، يمكنك فقط الضغط على F9. ستظهر نتيجة الحسابات في خانة Risk of Ruinفي شكل نسبة مئوية.

ستجد أسفل مدخلات الجدول صف يعرض أرقام الصفقات. أسفل هذا القسم هناك صفوف لأرصدة الحسابات الناتجة بعد كل صفقة، مع ملاحظة أن كل صف يمثل عملية محاكاة واحدة.

تضيف كل صفقة إما متوسط الربح أو تخصم متوسط الخسارة من الحساب بحسب ما إذا كان الرقم العشوائي الذي تم إنشائه لكل صفقة أقل أو أكبر من قيمة ’احتمال الربح‘. إذا وصل رصيد الحساب بعد صفقة معينة إلى الصفر أو قيمة سلبية، تتوقف عملية المحاكاة وتُظهر بدلاً من ذلك كلمة "مفلس".

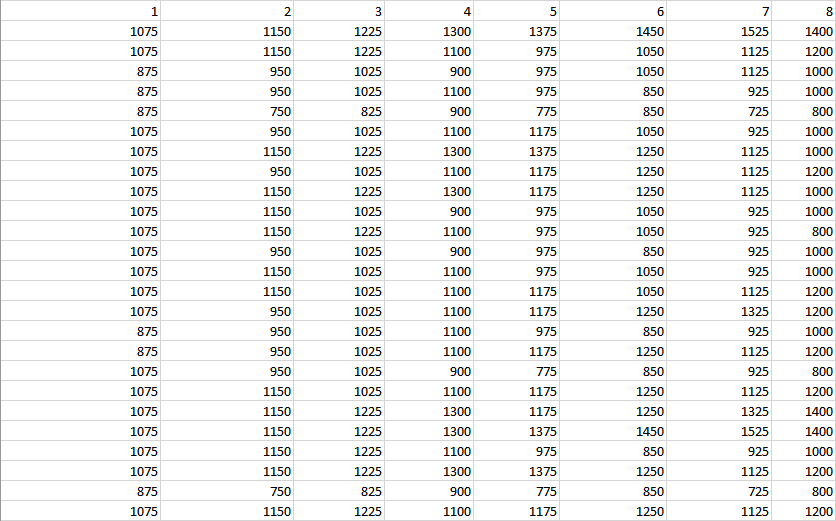
إذا كنت ترغب في الحصول على أكثر من الحد الأقصى لعدد المرات المسموح بها في جدول البيانات، أي 1,000، يمكنك بسهولة نسخ المزيد من الصفوف إلى أسفل —من المفترض أن تعمل المعادلات بشكل صحيح ودون مشاكل. وكما هي الحال مع عدد الصفقات لكل عملية محاكاة، يمكنك نسخ ولصق الأعمدة بعد الصفقة #1,000 لزيادة الحد الأقصى لعدد الصفقات.

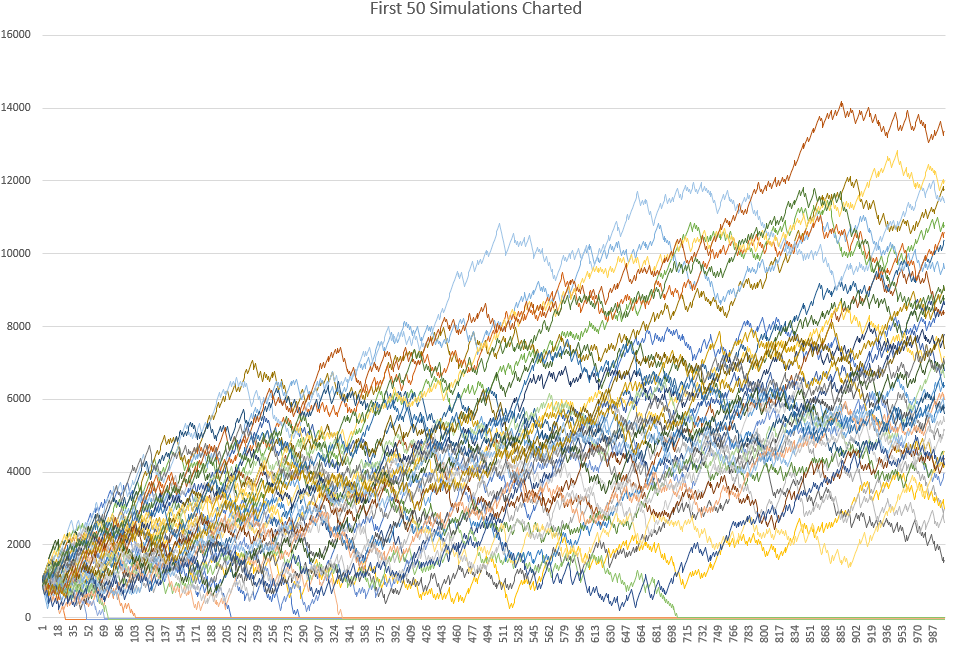
فيما يلي الرسم البياني مع مثال يعرض أول 50 محاكاة. لاحظ كيف يصل بعضها إلى خط الصفر ويبقى هناك — يشير ذلك إلى عمليات المحاكاة التي أدت فيها الاستراتيجية إلى تصفير حساب التداول:

المزايا

1. محاكاة مونت كارلو هي مفهوم بسيط للغاية ولا ينطوي على أي عمليات رياضية معقدة.
2. يساعد استخدام عمليات محاكاة متعددة مع متغيرات غير ثابتة على استخلاص احتمالات أكثر دقة للإفلاس مقارنةً باستخدام قيم المتوسطات البسيطة.
3. يتوفر على الإنترنت عدد كبير من الأدوات التي يمكن استخدامها في إجراء محاكاة مونت كارلو —يشمل ذلك العديد من مواقع الويب وإضافات إكسل.

العيوب

1. تفترض محاكاة مونت كارلو وجود ’سوق مثالي‘، بمعنى أنها لا تأخذ في الاعتبار التغيرات الأساسية، سواء تلك المتعلقة بأحداث هامة قصيرة المدى (مثل كوفيد-19) أو تغيرات طويلة المدى نتيجة تعديلات هيكلية في آلية عمل السوق (من أمثلة ذلك "ربط" ثم بعد ذلك "فك ربط" سعر صرف الفرنك السويسري مع اليورو بواسطة البنك الوطني السويسري). هذه التغيرات المؤثرة تجعل من البيانات التاريخية المستخدمة في الحساب عديمة الفائدة.
2. يمكن أن يؤدي تغيير استراتيجية تداولك أيضًا إلى جعل البيانات التاريخية غير ملائمة لإجراء تحليل الاحتمالات، ما يعني أن محاكاة مونت كارلو يمكن استخدامها فقط لاختبار استراتيجيات التداول المستمرة.
3. تفترض محاكاة مونت كاولو أن كل صفقة مستقلة عن سابقتها. ولهذا فهي غير مناسبة للاستراتيجيات التي تنطوي على سلاسل مترابطة وصفقات لا تأخذ في الاعتبار نتائج الصفقات السابقة.

خاتمة

لا يمكن أن نصف أي طريقة من الطرق التي ناقشناها أعلاه بأنها مثالية. بعبارة أخرى، ينبغي اختيار إحداها عندما تتناسب الطريقة مع معايير استراتيجية تداول الفوركس.

• معادلة حجم المركز الثابت مناسبة تمامًا إذا كنت تستخدم صفقات ذات أحجام ثابتة، وتستطيع حساب الانحراف المعياري، وكانت قيمة الإدخال للصفقات الخاسرة في الانحراف المعياري أكبر من قيمة الإدخال لتباين الصفقات الرابحة. تعتبر أيضًا طريقة جيدة إذا كنت لا تريد إجراء أي حسابات معقدة.
• معادلة تحديد حجم مركز التداول وفق نسبة ثابتة هي طريقة مثالية تمامًا لاستراتيجيات تحديد حجم الصفقات على أساس نسب كسرية. ومرة أخرى، يظل استخلاص الانحراف المعياري خطوة ضرورية، كما يتعين حسابه أيضًا لكلاً من الصفقات الرابحة والخاسرة.
• طريقة إفلاس المقامر نوصي باستخدامها إذا كنت واثقًا من أن المعلمات الإحصائية لنظام التداول مستقرة (حجم متوسط الربح/الخسارة، نسب الربح/الخسارة) ولا تمانع في إجراء بعض الحسابات المعقدة.

بغض النظر عن الطريقة التي تختارها، من المهم تذكر أن قيمة الاحتمال الناتجة ينبغي التعامل معها بحذر شديد. الغرض الرئيسي هو مقارنة الاستراتيجيات المختلفة أو تأثير التغيرات المطبقة على نفس استراتيجية التداول. الاعتماد على قيمة المخاطرة المحسوبة كمقياس حقيقي لمخاطر الاستراتيجية قد يؤدي إلى عواقب غير متوقعة ولا ينبغي التعامل معها على هذا النحو.

إذا كانت لديك أي أسئلة أو تعليقات بخصوص تقييم خطر الإفلاس في تداول الفوركس، فلا تتردد في مناقشتها في منتدانا.