Riesgo de ruina en trading
Contenido
Todo operador de Forex quiere saber qué riesgo tiene su estrategia y cuál es la posibilidad de perder una parte de la cuenta o todo el saldo. Esta posibilidad se llama riesgo de ruina. Como normalmente los operadores de Forex conocen su ratio de ganancias/pérdidas y el tamaño medio de sus posiciones ganadoras y perdedoras, calcular el riesgo de ruina debería ser relativamente fácil. ¿Verdad? Por desgracia, no es tan sencillo.
El riesgo de ruina es un problema conocido en la teoría de la probabilidad y, hasta cierto punto, puede resolverse utilizando las leyes y fórmulas de esta teoría. Evaluar el riesgo de ruina en el mercado de divisas es una tarea muy compleja que requiere mucha investigación y potencias de cálculo en dependencia exponencial del nivel de precisión deseado.
Las formas más populares de calcular el riesgo de ruina de una estrategia de Forex son dos fórmulas estáticas para el tamaño de posición fijo y el tamaño de posición fraccional fijo empleadas actualmente por muchas redes sociales de Forex (p. ej. FXSTAT, Myfxbook y otras). Las fórmulas fueron presentadas por D.R. Cox y H.D. Miller en La teoría de los procesos estocásticos y están disponibles públicamente en varias fuentes (p. ej. Minimizando su riesgo de ruina de David E. Chamness en el número de agosto de 2009 de la revista Futures Magazine). Pueden parecer muy complejos a primera vista, pero en realidad se pueden calcular con una calculadora o una hoja de cálculo de Excel.
Riesgo de ruina con un tamaño de posición fijo
La condición de tamaño de posición fijo sugiere que el operador de Forex no aumentará o disminuirá el tamaño de la posición después de obtener nuevas ganancias o pérdidas. Por ejemplo, si uno empieza con un saldo de cuenta de 10 000 $ y 1 lote estándar por posición, bajar a 1000 $ de saldo o avanzar a 50 000 $ de saldo no cambiará ese volumen de posición de 1 lote. La probabilidad de perder una parte del saldo es exponencialmente proporcional a la desviación estándar de la cuenta y es inversamente proporcional al tamaño de esta parte y al rendimiento medio por operación. La fórmula del riesgo de ruina es la siguiente:
donde:
- e es el número de Euler (~2,71828),
- A es el coeficiente de rendimiento medio por operación (por ejemplo, si sus posiciones han devuelto el 2% de su cuenta por término medio, entonces A = 0,02),
- Z es la parte de la cuenta cuyo riesgo de pérdida se está evaluando (p. ej., para calcular el riesgo de perder el 40% de una cuenta, Z = 0,4),
- D es la desviación estándar de los rendimientos de sus operaciones (debe calcularse de forma relativa, no en unidades monetarias).
Ejemplo 1:
El riesgo de perder el 10% del saldo de la cuenta, considerando una rentabilidad media del 2% en una posición y una desviación estándar del 7%:

Ejemplo 2:
El riesgo de ruina total (100% del saldo de la cuenta), considerando una rentabilidad media del 1,5% en una posición y una desviación estándar del 1%:
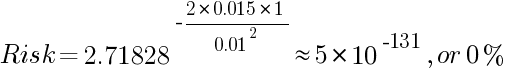
Es fácil darse cuenta que esta fórmula calcula el riesgo de ruina para un número infinito de operaciones. Según esto, el riesgo de pérdida siempre será del 100% para el sistema que actualmente muestra una expectativa negativa en la operativa y siempre será lo suficientemente cercano (pero no igual) a 0 para el rendimiento medio suficientemente alto y la desviación estándar suficientemente baja de los retornos.
Ventajas:
- Es un método muy sencillo. La fórmula se puede calcular con una calculadora. La desviación estándar es más complicada, pero si se conoce el saldo de la cuenta después de cada operación, solo se necesitan varios minutos para calcularla manualmente. Un ciclo simple puede calcularlo dentro de un asesor experto o algún otro script.
- El resultado es bastante preciso.
- Puede utilizarse para calcular el riesgo de pérdida de cualquier fracción de la cuenta.
Desventajas:
- Sustituye el "riesgo" real de las operaciones por la desviación estándar, lo que no es del todo correcto.
- Supone que la tasa de rendimiento actual y la desviación estándar no cambiarán con el tiempo. Una combinación de tasa de rendimiento constante y un tamaño de posición fijo es casi imposible en la vida real.
- Asume un tamaño de posición fijo, pero la pérdida de alguna parte de la cuenta de trading puede obligar a un operador de Forex a disminuir el tamaño de la posición (lo más probable es que no sea posible utilizar un tamaño de posición de lote estándar si la cuenta pasa de 10 000 a 800 $, por ejemplo).
- Muestra el riesgo para un número infinito de operaciones: nadie opera tanto tiempo.
- La precisión no es perfecta, incluso si todas las hipótesis son perfectamente válidas para una determinada estrategia de trading.
Riesgo de ruina con tamaño de posicionamiento fraccional fijo
A diferencia del modelo de tamaño de posición fijo, el tamaño de posición fraccional fijo implica que un operador arriesga una fracción fija de su cuenta por operación (por ejemplo, el 1%; el valor real no importa aquí), por lo que el beneficio es proporcional al tamaño de la cuenta y la pérdida es inversamente proporcional a él. Al igual que con el tamaño de posición fijo, la probabilidad de perder una parte del saldo sigue siendo inversamente proporcional al tamaño de esta parte. La dependencia del riesgo de la desviación estándar sigue siendo positiva, y del tamaño de la parte, sigue siendo negativa, pero su naturaleza se vuelve más compleja. La fórmula para el cálculo del riesgo es la siguiente:
donde:
- e es el número de Euler (~2,71828),
- A es el coeficiente de rendimiento medio por operación (por ejemplo, si las posiciones han devuelto el 14% de la cuenta por término medio, entonces A = 0,14),
- Z es la parte de la cuenta para la que se evalúa el riesgo de perder (por ejemplo, para calcular el riesgo de perder el 25% de la cuenta, Z = 0,25),
- D es la desviación estándar de los rendimientos de las operaciones (debe calcularse de forma relativa, no en unidades monetarias),
- ln es el logaritmo natural.
A continuación, se muestran dos ejemplos del cálculo del riesgo de ruina utilizando el modelo de tamaño de posición fraccional fijo con las mismas condiciones que para los ejemplos de tamaño de posición fijo anteriores:
Ejemplo 1:
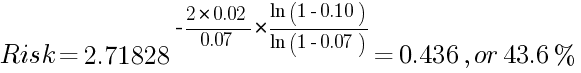
Obviamente, es solo ligeramente inferior al 44,2% del modelo de tamaño de posición fijo.
Ejemplo 2:
Dado que utilizar el 100% del saldo de la cuenta para la fórmula implicaría que Z = 1, habría un error en el cálculo del logaritmo natural (el logaritmo natural de 0 no está definido, pero es un número negativo infinitamente grande). Esto significa que es imposible perder toda la cuenta si la estrategia tiene una tasa de rendimiento positiva y se utiliza un tamaño de posición fraccional fijo:
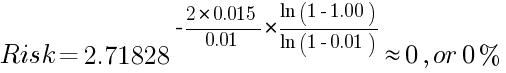
Evidentemente, esta fórmula muestra un riesgo menor porque asume un tamaño de posición fraccional, lo que reduce el tamaño de la posición en caso de pérdidas, reduciendo así las pérdidas posteriores y así sucesivamente.
Ventajas:
- Sigue siendo un método de evaluación del riesgo de ruina muy sencillo. En comparación con la fórmula de tamaño de posición fijo, solo se añaden algunos pasos nuevos, pero los datos utilizados son los mismos.
- El resultado es aún más preciso para su modelo de tamaño de posición.
- También puede utilizarse para calcular el riesgo de pérdida de cualquier fracción de la cuenta.
Desventajas:
- Al igual que en la fórmula del tamaño de posición fijo, el riesgo real se sustituye por la desviación estándar.
- Supone una tasa de rendimiento y una desviación estándar constantes.
- Calcula el riesgo para un número infinito de operaciones.
Problema de la ruina del jugador mediante cadenas de Markov
El método más intuitivo para calcular el riesgo de pérdida resulta ser el más difícil en términos de cálculos reales. El problema del riesgo de ruina en el mercado Forex puede definirse como un caso particular del problema de ruina del jugador, en el que un operador (jugador), partiendo de un saldo de cuenta inicial (apuesta), tiene una determinada probabilidad de ganar una cantidad media de beneficios determinada y una probabilidad diferente (o, a veces, la misma) de perder una cantidad media de pérdidas determinada. El operador está compitiendo contra el mercado (un adversario infinitamente rico). Por lo tanto, solo el operador puede conseguir que el saldo de la cuenta se arruine; la condición de ganar puede definirse como alcanzar algún saldo objetivo superior al inicial.
En el capítulo 12 de la obra Introducción a la probabilidad de Charles M. Grinstead y J. Laurie Snell, se puede encontrar más información sobre las fórmulas sencillas de cálculo del riesgo de pérdida con este método.
Ganar es igual que perder, las mismas probabilidades
En el caso de que el beneficio medio sea igual a la pérdida media y la probabilidad de perder sea igual a la probabilidad de ganar, la tarea de calcular el riesgo exacto de ruina es extremadamente sencilla. El saldo inicial se denomina z y el saldo objetivo se denomina M. El riesgo de arruinar la cuenta antes de pasar de z a M sería entonces:

Ejemplo 1:
El saldo inicial es de 10 000 $ (z). Hay una probabilidad de 50/50 de perder o ganar 1000 $ con cada operación. El saldo objetivo es de 20 000 $ (M):
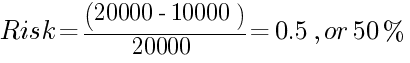
Obviamente, la probabilidad de subir de 10 000 a 20 000 $ es la misma que la de bajar a 0 $.
Ganar es igual que perder, diferentes probabilidades
La probabilidad de ganar (p) es la posibilidad de ganar (terminar con ganancias) una posición. Sería muy interesante que los operadores pudieran conocer sus probabilidades exactas de ganar una determinada operación, pero en lugar de ello se deben utilizar aquí los ratios de ganancias/pérdidas. El número de operaciones rentables dividido por el número total de operaciones se utilizará como la probabilidad de ganar. Es seguro incluir aquí las posiciones con
La probabilidad de perder (q) es la posibilidad de perder (terminar con una pérdida) una posición. Por las mismas razones anteriores, la mejor estimación que se puede utilizar aquí es una simple relación de ganancias y pérdidas. q = Número de operaciones perdedoras / Número total de operaciones. Obviamente, si las posiciones de beneficio cero se contabilizaron en el cálculo de p, no deben incluirse aquí.
Si la probabilidad de ganar una determinada operación no es la misma que la de perderla, entonces hay que utilizar una fórmula un poco más compleja. La probabilidad de ganar una operación rentable promedio es p, la probabilidad de perder una operación: q (p + q = 1). Entonces, el riesgo de ruina se calcula de la siguiente manera:
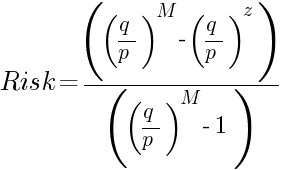
Ejemplo 2:
El saldo inicial es el mismo, 10 000 $ (z), el objetivo también es el mismo, 20 000 $ (M) y la media de ganancias/pérdidas es la misma, 1000 $ por operación, pero ahora la probabilidad de ganar es de 0,55 y la de perder es de 0,45 (un sistema de trading con una ventaja del 5%). Para simplificar los cálculos, es totalmente seguro dividir los saldos inicial y objetivo por la media de ganancias/pérdidas para obtener z = 10 y M = 20. El riesgo de ruina antes de duplicar el saldo se calcula de la siguiente manera:
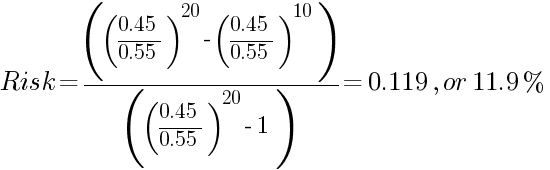
Evidentemente, una ventaja del 5% proporciona a un operador de Forex una enorme mejora en la fiabilidad de todo el sistema de trading.
Diferentes tamaños de ganancias y pérdidas, diferentes probabilidades
En realidad, una estrategia de trading de Forex rara vez opera con un beneficio medio que sea igual a la pérdida media. La diferencia en los resultados de las posiciones ganadoras y perdedoras conduce a una complejidad mucho mayor en el cálculo del riesgo de ruina. No tiene sentido exponer aquí todo el algoritmo de cálculo en detalle para este caso. En su lugar, es mejor proporcionar una visión general de los pasos necesarios, que pueden reducirse fácilmente a problemas matemáticos o de programación triviales.
Matemáticas
La información detallada sobre las matemáticas del cálculo del riesgo de ruina para el caso general (diferentes tamaños y probabilidades de ganancia/pérdida) se puede encontrar en el artículo de Kevin Brown La ruina del jugador. Es una obra magnífica que ofrece una excelente explicación de este problema y de las formas de solucionarlo.
El proceso de trading puede representarse como un modelo de Markov
En general, la fórmula de la probabilidad de arruinar toda la cuenta antes de alcanzar un saldo objetivo puede escribirse como sigue:
![Riesgo = ([q...(q)(0...0)(0)...0]M^-1Cj)/([q...(q)(0...0)(p)...p]M^-1Cj) Riesgo = ([q...(q)(0...0)(0)...0]M^-1Cj)/([q...(q)(0...0)(p)...p]M^-1Cj)](/img/articles/blog/2011/10/gamblers-ruin-general-case-matrix-risk-of-ruin.png)
donde:
- p es la probabilidad de ganar una operación.
- q es la probabilidad de perder una operación.
- El
vector fila superior (un vector perdedor) es de la longitud k. Los primeros elementos de pérdida media / MCD (paso de pérdida) son q, los demás son 0. - El
vector fila inferior (un vector total) también es de la longitud k. Los primeros elementos de pérdida media / MCD (paso de pérdida) son q, los últimos elementos de beneficio medio / MCD (paso de ganancia) son p, el resto son 0. - M-1 es la matriz inversa de la matriz de coeficientes M. M es una matriz k×k que tiene 1 en todos sus elementos diagonales principales. Además del 1 de la diagonal, cada columna puede contener hasta dos elementos
distintos de cero : -p, situado por debajo de la diagonal principal, con el desplazamiento vertical desde ella igual al paso de ganancia; -q, situado por encima de la diagonal principal, con el desplazamiento vertical desde ella igual al paso de pérdida. - Cj es la matriz (vector)
de columna única de tamaño k donde todos los elementos son iguales a 0, excepto el elemento en la posición j (estado inicial), que es igual a 1.
En el ejemplo anterior, la matriz M tendría el siguiente aspecto:
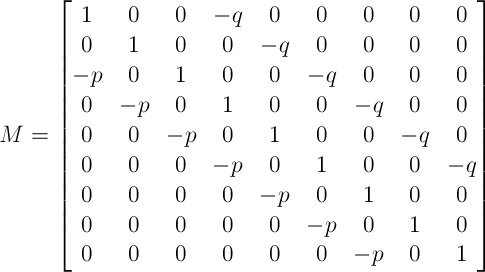
Y si se rellena con valores:

Y el vector Cj quedaría así:
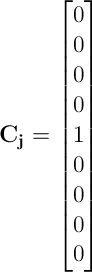
Mientras que la multiplicación de matrices/vectores es trivial, invertir una matriz mayor que
Optimización
El ejemplo es bastante sencillo, la matriz es solo de 9×9 y su inversa se puede calcular bastante rápido sin ninguna optimización. ¿Pero qué pasa si el MCD de la estrategia es de 1 $? Por ejemplo, si la pérdida media es de 1113 $ y el beneficio medio es de 1109 $, el MCD es de 1 $. Con un saldo inicial de 2500 $ y un objetivo de 5000 $, se trata de una matriz de
En primer lugar, es importante que la matriz M-1 sea lo más pequeña posible. Lo óptimo es que k sea inferior a 500 si el objetivo es resolver este problema en un tiempo razonable (varios segundos).
En segundo lugar, la memoria requerida puede reducirse significativamente: el vector perdedor puede almacenarse dentro del vector total (se sabe dónde terminan las q del vector perdedor y comienzan los 0) y los resultados de la descomposición LU pueden almacenarse dentro de la matriz principal (M: puede descartarse después de la descomposición).
En tercer lugar, tanto Ly = I como Ux = y pueden resolverse para una columna (jª), en lugar de toda la matriz k×k. Esa misma columna será también el resultado de la multiplicación con Cj. Esto se debe a que, si se calcula toda la matriz k×k y luego se multiplica por Cj, el resultado también será solo la jª columna de la matriz, debido a todos los ceros en Cj.
Por último, es posible calcular el producto del vector perdedor con la jª columna y el producto del vector total con esa columna simultáneamente, ya que las iteraciones del primer paso de pérdida serán las mismas durante ese cálculo, mientras que las demás iteraciones no serán necesarias en el caso del vector perdedor.
Implementación
Aquí está el código PHP de ejemplo que utiliza el algoritmo de arriba para encontrar el riesgo de ruina para el ejemplo anterior:
/* Saldo inicial: 2500 $ Saldo objetivo: 5000 $ Operación perdedora media: 1500 $ Operación rentable media: 1000 $ Probabilidad de pérdida: 30% Probabilidad de ganancia: 70% */ // Máximo común divisor = 500 $. $begin_state = 5; // Saldo inicial dividido por el MCD. $N = 9; // El número de estados transitorios; k en el artículo. $loss_step = 3; // El tamaño de la pérdida se divide por el MCD. $win_step = 2; // El tamaño de la ganancia se divide por el MCD. $q = 0.3; // Probabilidad de pérdida. $p = 0.7; // Probabilidad de ganancia. // Rellenando el vector Cj. for ($i = 0; $i < $N; $i++) if ($i == $begin_state - 1) $unitary_vector[$i] = 1; else $unitary_vector[$i] = 0; // Rellenando el vector de pérdidas y el vector total. El vector de pérdidas es en realidad una parte del vector total. for ($i = 0; $i < $N; $i++) if (($i - $loss_step) < 0) $total_vector[$i] = $q; else if (($i + $win_step) >= $N) $total_vector[$i] = $p; else $total_vector[$i] = 0; // Rellenando la matriz principal. for ($i = 0; $i < $N; $i++) for ($j = 0; $j < $N; $j++) // La diagonal principal es siempre 1. if ($i == $j) $a[$i][$j] = 1; // Los elementos por encima de la diagonal principal representan pérdidas. else if ($j == $i + $loss_step) $a[$i][$j] = -$q; // Los elementos por debajo de la diagonal principal representan ganancias. else if ($j == $i - $win_step) $a[$i][$j] = -$p; else $a[$i][$j] = 0; // La descomposición LU. for ($i = 0; $i < $N; $i++) { for ($j = $i; $j < min($N, $i + $loss_step); $j++) // U for ($k = 0; $k <= $i - 1; $k++) $a[$i][$j] -= $a[$i][$k] * $a[$k][$j]; for ($j = $i + 1; $j <= min($i + $win_step, $N - 1); $j++) // L { for ($k = 0; $k <= $i - 1; $k++) $a[$j][$i] -= $a[$j][$k] * $a[$k][$i]; $a[$j][$i] /= $a[$i][$i]; } } // Resolviendo Ly = I para una columna (unitary_vector) que es igual a Cj de la fórmula de la ruina del jugador. // La y resultante también se almacenará en unitary_vector. // Comienza desde begin_state porque todas las X antes de 1 en el unitary_vector siempre serán 0. for ($i = $begin_state; $i < $N; $i++) { $sum = 0; for ($j = 0; $j <= $i - 1; $j++) $sum -= $a[$i][$j] * $unitary_vector[$j]; $unitary_vector[$i] = $unitary_vector[$i] + $sum; } // Resolviendo Ux = y para una columna que fue calculada en Ly = I. // La x resultante se almacenará en unitary_vector. for ($i = $N - 1; $i >= 0; $i--) { $sum = 0; for ($j = $N - 1; $j > $i; $j--) $sum -= $a[$i][$j] * $unitary_vector[$j]; $unitary_vector[$i] = ($unitary_vector[$i] + $sum) / $a[$i][$i]; } // Multiplicando total_vector y su parte perdedora por el unitary_vector resultante. $loss = 0; $total = 0; for ($i = 0; $i < $N; $i++) { $product = $total_vector[$i] * $unitary_vector[$i]; if (($i - $loss_step) < 0) $loss += $product; $total += $product; } $probability = $loss / $total; echo "Pérdida: $loss <br>"; echo "Total: $total <br>"; echo "Probabilidad: $probability <br>";
Con lo que se mostraría:
Pérdida: 0,25755603952 Total: 1 Probabilidad: 0,25755603952
Por lo tanto, el riesgo de arruinar toda la cuenta antes de duplicarla es de aproximadamente el 25,8% para este ejemplo.
Pero, ¿y si k se hace demasiado grande? En este caso, debe aplicarse un redondeo matemático al paso de pérdidas, al paso de ganancias y a los saldos inicial y objetivo, truncando virtualmente algunos de los últimos dígitos. Además, el saldo objetivo puede reducirse. El primer método influye en la precisión, pero su efecto es menos importante a medida que aumenta la diferencia entre la pérdida media y el beneficio medio.
Ventajas
- Si se asume que los datos de entrada (las probabilidades y el tamaño de las ganancias/pérdidas) son 100% exactos, entonces este método ofrece un resultado perfectamente preciso.
- No depende del método de tamaño de la posición, sino de la pérdida/ganancia media resultante en números absolutos: las estadísticas fácilmente disponibles en todos los informes de estrategias de Forex.
- Otros parámetros de entrada también son muy sencillos: no es necesario calcular la desviación estándar.
- Los casos sencillos pueden calcularse manualmente.
- El riesgo calculado es "perderlo todo antes de alcanzar el saldo objetivo", algo alcanzable en contraste con el "número infinito de operaciones" de los métodos anteriores.
Desventajas
- Supone que los principales parámetros de la estrategia de trading (los tamaños y los porcentajes de ganancias/pérdidas) no cambian. Eso casi nunca es así en el mundo real.
- Es un método muy complejo.
- En muchos casos, requiere mucha potencia de cálculo o mucho redondeo, lo que reduce la precisión del resultado.
Riesgo de ruina con la simulación de Monte Carlo
La simulación de Montecarlo (también conocida como método de Montecarlo) es un modelo que predice la probabilidad de diferentes resultados que implican variables aleatorias. Inventado por el matemático Stanislaw Ulam, lleva el nombre de Montecarlo, un popular lugar de juego en Mónaco. El nombre parece apropiado, ya que los juegos de azar suelen asociarse con el azar y los resultados aleatorios.
La esencia del método de Montecarlo es simular el resultado muchas veces con variables aleatorias que obtienen nuevos valores en cada simulación. Para entender mejor cómo funciona el método, veamos una situación hipotética.
Utilizando datos históricos y backtests, ha calculado la probabilidad de pérdida o ganancia para una operación media con su estrategia de trading, así como el tamaño medio de sus ganancias y pérdidas. ¿Cómo calcular el riesgo de ruina con estos datos? Puede tratar de simular un resultado, aleatorizando cada operación y comprobando si el saldo de su cuenta desaparecerá al final. Pero una simulación no sirve de mucho, ya que solo muestra un resultado entre muchas posibilidades y no dice que sea probable.
¿Pero qué pasa si se simula el resultado cien veces? ¿Mil? ¿Diez mil? El método de Montecarlo sugiere que, al aleatorizar el resultado de cada operación (una ganancia o una pérdida y, posiblemente, el tamaño de la ganancia o la pérdida), se obtienen valiosos datos estadísticos al volver a ejecutar dichas simulaciones. Y cuantas más simulaciones se realicen, más fiables serán los datos. En el caso del trading de Forex, si se observa cuántas veces el uso de su estrategia ha resultado en la desaparición total del saldo de su cuenta, se puede determinar el riesgo de ruina.
Ejemplo de simulación de Montecarlo en una hoja de cálculo de Excel
Esta hoja de cálculo de Excel muestra un ejemplo de una simple simulación de Montecarlo. Supone que usted conoce la probabilidad de una operación ganadora, así como el tamaño de la ganancia media y la pérdida media.
Introduzca el importe del saldo de su cuenta en el campo Saldo inicial de la cuenta. Introduzca la probabilidad de ganancia en el campo Probabilidad de ganancia como un número de 0 a 1. Por ejemplo, si la probabilidad de ganancia es del 65%, deberá introducir 0,65. A continuación, introduzca la ganancia media y la pérdida media en el campo correspondiente. Si desea utilizar un rango en lugar de un número medio fijo, puede hacerlo fácilmente utilizando la función RANDBETWEEN. A continuación, introduzca el número deseado de operaciones simuladas y el número de simulaciones en los campos Nº de operaciones y Nº de simulaciones, respectivamente. Después de rellenar todos los campos, puede calcular el riesgo de ruina. Para ello, vaya a Fórmulas en el menú principal del Excel y haga clic en Calcular ahora a la derecha de Opciones de cálculo. También puede pulsar
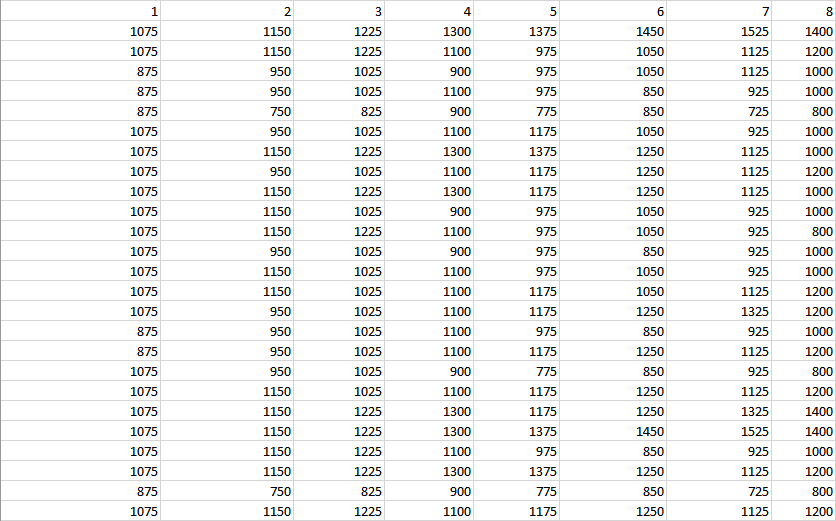
Debajo de las entradas de la tabla, verá la fila de los números de las operaciones. Debajo, hay filas de los saldos de cuenta resultantes en cada operación, y cada fila representa una simulación.
Cada operación añade la cantidad de ganancia media o resta la cantidad de pérdida media de la cuenta, dependiendo de si el número aleatorio generado para esa operación está por debajo o por encima del valor de la probabilidad de ganancia. Si, en alguna operación, el saldo de la cuenta alcanza un valor cero o negativo, esa simulación se detiene y se cuenta como "arruinada".
Si quiere tener más simulaciones que el máximo de 1000 posibles con la hoja de cálculo dada, puede copiar fácilmente las filas más abajo; las fórmulas deberían funcionar correctamente. Lo mismo con el número de operaciones por simulación, puede copiar y pegar las columnas después de la operación n. º 1000 para aumentar el número máximo de operaciones.
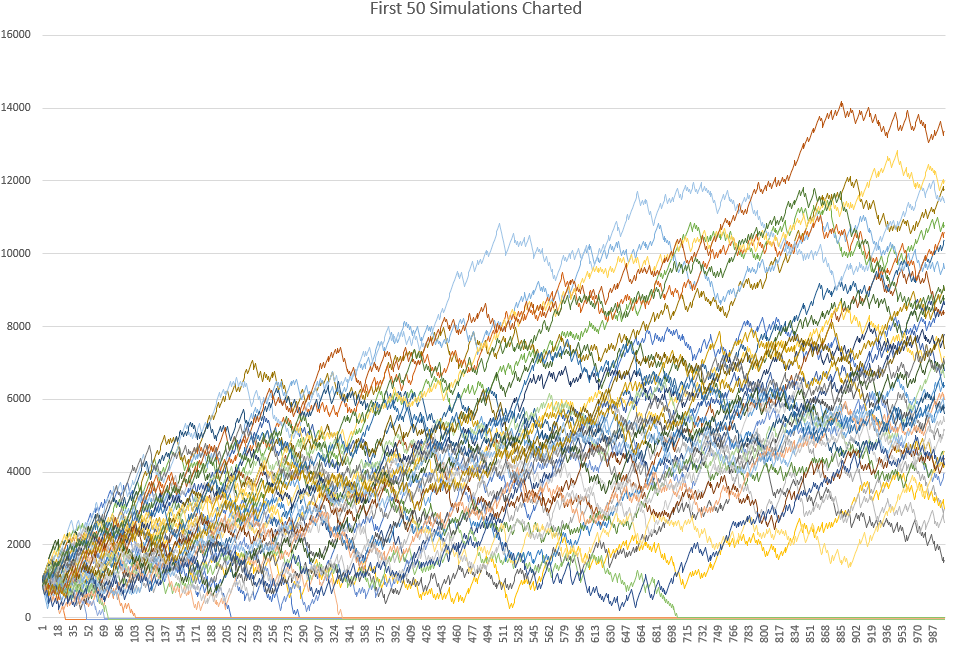
Aquí está el gráfico con un ejemplo de las primeras 50 simulaciones trazadas. Obsérvese cómo algunas de ellas alcanzan la línea cero y permanecen allí: son simulaciones en las que la estrategia arruinó la cuenta de trading:
Ventajas
- La simulación de Montecarlo es un concepto sencillo y no implica matemáticas complejas.
- Utilizando múltiples simulaciones con variables cambiantes, se puede obtener una probabilidad de ruina más precisa que utilizando simples valores medios.
- Hay muchas herramientas en Internet para realizar simulaciones de Montecarlo, desde páginas web hasta complementos de Excel.
Desventajas
- La simulación de Montecarlo parte de un "mercado perfecto", lo que significa que no tiene en cuenta los cambios fundamentales, ya sean cambios a corto plazo debidos a acontecimientos importantes (como la COVID-19) o cambios a largo plazo debidos a cambios estructurales en el funcionamiento del mercado (el ejemplo de esto es la "vinculación" y la posterior "desvinculación" del franco suizo al euro por parte del Banco Nacional de Suiza). Estos cambios hacen inútiles los datos históricos utilizados para los cálculos.
- Los cambios en la estrategia de trading también pueden hacer que los datos históricos sean irrelevantes, lo que significa que la simulación de Montecarlo debe utilizarse únicamente para probar estrategias de trading coherentes.
- La simulación de Montecarlo supone que cada operación es independiente de las anteriores. Por lo tanto, es inadecuado para estrategias correlacionadas en serie con operaciones que tienen en cuenta los resultados de las operaciones anteriores.
Conclusión
Ninguno de los métodos descritos es perfecto. Cada uno de ellos debe utilizarse únicamente cuando se ajuste a los parámetros de la estrategia de trading de Forex:
- La fórmula del tamaño de posición fijo es buena cuando se sabe que el tamaño de la posición es fijo, se puede calcular la desviación estándar y la entrada de las posiciones perdedoras en la desviación estándar es mayor que la de la variabilidad de las posiciones ganadoras. Es un buen método si no quiere realizar ningún cálculo complejo.
- La fórmula del tamaño de posición fraccional fijo es perfecta para las estrategias que usan tamaños de posición fraccionales. De nuevo, es necesario encontrar la desviación estándar. También debe estar formado por las posiciones perdedoras y ganadoras.
- El método de la ruina del jugador se recomienda cuando se está seguro de que los parámetros estadísticos del sistema de trading son estables (el tamaño medio de las ganancias/pérdidas, los porcentajes de ganancias/pérdidas) y no le importa hacer algunos cálculos realmente complejos.
Sea cual sea el método elegido, es importante recordar que el valor de riesgo resultante no debe tomarse demasiado en serio por sí solo. Su principal objetivo es comparar diferentes estrategias o el efecto de los cambios aplicados a una estrategia de trading. Confiar en el valor de riesgo calculado como la verdadera medida de la peligrosidad de la estrategia puede llevar a consecuencias inesperadas pero horribles.
Si tiene alguna pregunta o comentario sobre la evaluación del riesgo de ruina en el trading de Forex, no dude en comentarlo en nuestro foro.