Риск разорения в торговле

Каждый Форекс-трейдер хочет знать, насколько рискованна его стратегия и какова вероятность потери части или всего остатка на счете. Эта вероятность называется риском разорения. Поскольку обычно Форекс-трейдеры знают свое соотношение прибыли/убытков и средний размер их прибыльных и убыточных позиций, расчет риска разорения должен быть сравнительно несложным. Или не должен? К сожалению, все не так просто.

Риск разорения – известная проблема в теории вероятности и может быть в какой-то мере решена с помощью законов и формул этой теории. Оценка риска разорения на Форексе – очень сложная задача, требующая значительных исследований и возможностей для расчета, прямо пропорциональных желаемой степени точности.

Чаще всего для расчета риска разорения, связанного со стратегией торговли на Форексе, используются две статичные формулы для фиксированного размера позиции и определения фиксированного дробного размера позиции; они применяются сегодня многими социальными сетями Форекс-трейдеров (например, FXSTAT, Myfxbook и другими). Эти формулы предложены Д. Р. Коксом и Х. Д. Миллером в Теории стохастических процессов и опубликованы во многих источниках (например, в статье Минимизация риска разорения Дэвида Чемнесса в августовском выпуске журнала "Фьючерсы" за 2009 г.). На первый взгляд они кажутся очень сложными, но на самом деле расчеты по этим формулам можно провести на калькуляторе или в таблице Excel.

Риск разорения с фиксированным размером позиции

Условие фиксированного размера позиции предполагает, что Форекс-трейдер не будет увеличивать или уменьшать размер позиции за счет новой прибыли или убытков. Например, если кто-то начнет с остатком на счете $10 000 и одним стандартным лотом на позицию, уменьшение остатка до $1 000 или его увеличение до $50 000 не изменит этот объем позиции в 1 лот. Вероятность потери части остатка прямо экспоненциально пропорциональна стандартному отклонению счета и обратно экспоненциально пропорциональна размеру этой части и средней доходности одной сделки. Риск разорения рассчитывается по формуле:

где:

• e – число Эйлера (~2,71828),
• A – средняя доходность сделки (например, если доходность ваших позиций в среднем 2% вашего счета, то A = 0,02),
• Z – часть счета, риск потери которой вы оцениваете (например, если рассчитывается риск потери 40% счета, то Z = 0,4),
• D – стандартное отклонение доходности ваших сделок (рассчитываемой как относительный показатель, а не в единицах валюты).

 

Пример 1:

Риск потери 10% остатка на счете, учитывая 2-процентную медианную доходность по позиции и стандартное отклонение 7%:

Пример 2:

Риск полного разорения (потери 100% остатка на счете), учитывая 1,5-процентную медианную доходность по позиции и стандартное отклонение 1%:

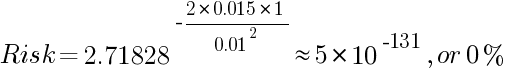
Легко заметить, что это формула для расчета риска разорения для бесконечного количества сделок. Согласно этой формуле, риск понести убытки всегда будет составлять 100% для системы, показывающей в настоящее время отрицательную ожидаемую среднюю прибыль по сделкам, и всегда будет достаточно близким к 0 (но не нулевым) для достаточно высокой медианной доходности и достаточно низкого стандартного отклонения доходности.

Преимущества:

1. это очень простая процедура. Расчеты по самой формуле можно провести на калькуляторе. Расчет стандартного отклонения сложнее, но если остаток на счете после каждой сделки известен, то его расчет вручную займет всего несколько минут. Простой цикл может рассчитать его в торговом советнике или каком-то ином скрипте.
2. Результат будет довольно точным.
3. Его можно использовать для расчета риска потери любой доли остатка на счете.

Недостатки:

1. Подменяет реальную "рискованность" сделок стандартным отклонением, что не вполне корректно.
2. Исходит из того, что текущие доходность и стандартное отклонение не изменятся со временем. Сочетание постоянной доходности с фиксированным размером позиции в реальной жизни практически не встречается.
3. Делается допущение, что размер позиции фиксирован, но потеря части остатка на счете может заставить Форекс-трейдера уменьшить размер позиции (скорей всего, будет невозможно использовать размер позиции в 1 стандартный лот, если остаток на счете уменьшится, например, с $10 000 до $800).
4. Показывает риск для бесконечного количества сделок в то время, как никто не торгует так долго.
5. Точность неидеальна, даже если все допущения идеально подходят для данной торговой стратегии.

Риск разорения с определением фиксированного размера дробной позиции

В отличие от модели фиксированного размера позиции, определение фиксированного дробного размера позиции подразумевает, что трейдер рискует фиксированной долей своего счета в расчете на одну сделку (например, 1%; реальная цифра здесь не очень-то важна), поэтому прибыль пропорциональна, а убытки – обратно пропорциональны остатку на счете. Как и с фиксированным размером позиции, вероятность утратить часть остатка по-прежнему обратно экспоненциально пропорциональна размеру этой части. Зависимость риска от стандартного отклонения по-прежнему положительна, а от размера этой части – по-прежнему отрицательна, но ее характер более сложен. Риск рассчитывается по формуле:

где:

• e – число Эйлера (~2,71828),
• A – средняя доходность одной сделки (например, если прибыль от ваших позиций составляет в среднем 14% вашего счета, то A = 0,14),
• Z – часть счета, риск потери которой оценивается (например, если рассчитывается риск потери 25% счета, то Z = 0,25),
• D – стандартное отклонение доходности сделок (рассчитываемой как относительный показатель, а не в единицах валюты),
• ln – натуральный логарифм.

Ниже приводятся два примера расчета риска разорения с помощью модели определения фиксированного дробного размера позиции с теми же условиями, что и для приведенных выше примеров фиксированного размера позиции:

 

Пример 1:

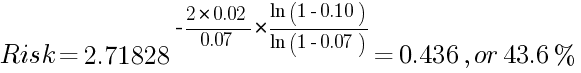
Очевидно, что этот показатель лишь чуть-чуть ниже 44,2%, полученных с помощью модели фиксированного размера позиции.

Пример 2:

Поскольку использование 100-процентной доли остатка на счете в этой формуле означало бы, что Z = 1, в расчете натурального логарифма произошла бы ошибка (натуральный логарифм 0 не определен, но это бесконечно большое отрицательное число). Это означает, что невозможно потерять весь остаток на счете, если у стратегии положительная доходность, и используется определение фиксированного дробного размера позиции:

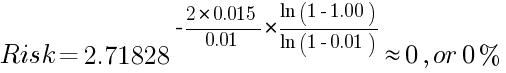
Очевидно, что эта формула показывает более низкий риск, так как исходит из определения дробного размера позиции, которое уменьшает размер позиции в случае убытков и тем самым снижает дальнейшие убытки и т.п.

Преимущества:

1. это все равно очень простой способ оценки риска разорения. По сравнению с формулой фиксированного размера позиции выполняется всего несколько новых шагов, но данные используются те же.
2. А результат расчетов по модели определения размера даже более точен.
3. Можно использовать и для расчета риска потери любой доли остатка на счете.

Недостатки:

1. Так же, как и в формуле фиксированного размера позиции, реальный риск подменяется стандартным отклонением.
2. Делается допущение о постоянстве доходности и стандартного отклонения.
3. Рассчитывается риск разорения для бесконечного количества сделок.

Задача о разорении игрока при применении цепей Маркова

Самый интуитивно понятный способ расчета риска убытков оказывается и самым трудным с точки зрения реально требуемых расчетов. Проблема риска разорения на Форексе может считаться частным случаем задачи о разорении игрока, в котором у трейдера (игрока), начинающего с начальным остатком на счету (ставкой), есть определенная вероятность выиграть и получить данную среднюю сумму прибыли и другая (а иногда и такая же) вероятность проиграть и понести убытки в размере данной средней суммы. Трейдер конкурирует с другими участниками рынка (как бесконечно богатый противник), поэтому только трейдер может лишиться остатка на счете; условие получения им прибыли можно определить как достижение определенного целевого остатка, превышающего начальный.

Более подробный предварительный анализ для простых формул расчета риска убытков этим способом можно найти в главе 12 Введения в вероятность Чарльза Гринстеда и Джеймса Лори Снеллом.

Прибыль равна убыткам, одинаковые вероятности

В случае, когда средняя прибыль равна средним убыткам, а вероятность понести убыток равна вероятности получения прибыли, задача точного расчета риска разорения очень проста. Начальный остаток обозначается z, a целевой остаток обозначается M. Тогда риск потери остатка на счете до превращения z в M составит:

 

Пример 1:

Начальный остаток – $10 000 (z): существует 50-процентная вероятность потери или получения $1 000 на каждой сделке. Целевой остаток (M) – $20 000:

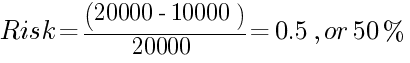
Достаточно очевидно, что вероятность увеличения остатка в $10 000 до $20 000 такая же, как и вероятность его снижения до $0.

Прибыль равна убыткам, разные вероятности

Вероятность получения прибыли (p) – это шанс выиграть (получить в итоге прибыль) на одной позиции. Было бы очень интересно, если бы трейдеры могли точно знать вероятность выиграть конкретную сделку, но взамен здесь должны использоваться коэффициенты прибыли/убытка. Количество прибыльных сделок, деленное на общее количество сделок, будет использоваться как вероятность получения прибыли. Ничто не мешает включить сюда позиции с нулевой прибылью, поскольку они будут компенсироваться средним размером прибыли, необходимо только не забыть учесть эти позиции при расчете прибыли.

Вероятность убытка (q) – это шанс проиграть (получить в итоге убытки) на одной позиции. По тем же причинам, что указаны выше, простой коэффициент прибыли/убытка – лучшая оценка, которую можно здесь использовать. q = Количество убыточных сделок/Общее количество сделок. Очевидно, что если учитывать позиции с нулевой прибылью при расчете p, то при расчете q их учитывать не нужно.

Если вероятность получения прибыли при проведении конкретной сделки отличается от вероятности понести убыток, то нужно использовать несколько более сложную формулу. Вероятность получения от сделки средней прибыли – это p, а вероятность понести убыток – это q (p + q = 1). Тогда риск разорения рассчитывается следующим образом:

 

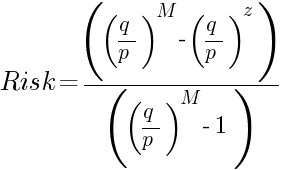
Пример 2:

Начальный остаток тот же $10 000 (z), цель та же $20 000 (M) и средняя прибыль/убыток тот же $1 000 со сделки, но теперь вероятность получения прибыли 0,55, а вероятность понести убыток 0,45 (торговая стратегия с преимуществом 5%). Для упрощения расчетов мы вполне можем разделить и начальный, и целевой остаток на среднюю прибыль/убыток и получить z = 10 и M = 20. Риск разорения до удвоения остатка рассчитывается следующим образом:

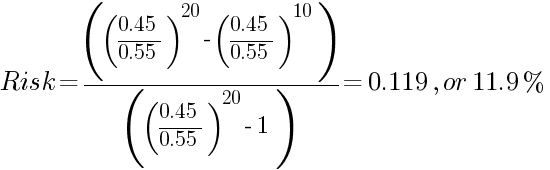
Очевидно, что преимущество 5% дает Форекс-трейдеру огромное повышение надежности всей торговой стратегии.

Разный размер прибыли/убытков, неодинаковые вероятности

На практике стратегия торговли на Форексе редко когда характеризуется тем, что средняя прибыль равна средним убыткам. Разница в результатах по прибыльным и убыточным позициям приводит к тому, что расчет риска разорения становится намного более сложным. Мы не станем приводить здесь весь алгоритм расчета для этого случая в деталях. Взамен мы расскажем о необходимых шагах, которые легко можно свести к тривиальным проблемам математики/программирования.

Математика

Подробную информацию о математике расчета риска разорения для общего случая (разные размеры прибыли/убытка и разные вероятности) можно найти в статье Кевина Брауна Разорение игрока. Это превосходная работа, содержащая блестящее объяснение этой проблемы и способов ее решения.

Процесс торговли можно представить как замкнутую модель Маркова с одним начальным состоянием (начальным остатком, например $2 500) и двумя конечными состояниями, нулевым и вашим целевым остатком (например $5 000). Имеется также число k – число переходных состояний, которое зависит от наибольший общего делителя (НОД) среднего прибыли и среднего убытка. Например, если средняя прибыль $1 000, а средний убыток $1 500, то их НОД – $500, и имеются 9 переходных состояний (k = 9), включая начальное. У двух последних переходных состояний ($4 000 и $4 500) имеется вероятность p достижения целевого остатка, а у первых трех состояний ($500, $1 000 и $1 500) имеется вероятность q разорения счета (снижения остатка до $0).

В общем виде формулу вероятность разорения всего счета до достижения целевого остатка можно записать следующим образом:

где:

• p – вероятность того, что сделка будет прибыльной.
• q – вероятность того, что сделка будет убыточной.
• Верхний вектор -строка (убыточный вектор) имеет длину k. Первые элементы Средний убыток / НОД (убыточный шаг) составляют q, а другие равны 0.
• Нижний вектор -строка (общий вектор) также имеет длину k. Первые элементы Средний убыток / НОД (убыточный шаг) составляют q, а последние элементы Средняя прибыль / НОД (прибыльный шаг) составляют p, а остальные равны 0.
• M^-1 – обратная матрица матрицы коэффициентов M. M – это k×k матрица, у которой во всех элементах ее главной диагонали находятся единицы. Помимо единиц по диагонали, каждый столбец может содержать до двух элементов, отличных от нуля: -p, находящееся ниже главной диагонали, с вертикальным смещением от нее, равным прибыльному шагу; -q, находящееся выше главной диагонали, с вертикальным смещением от нее, равным убыточному шагу.
• C_j – матрица из одного столбца (вектор) размера k, все элементы которой равны 0, кроме элемента в позиции j (начальное состояние), который равен 1.

В вышеприведенном примере матрица M выглядела бы следующим образом:

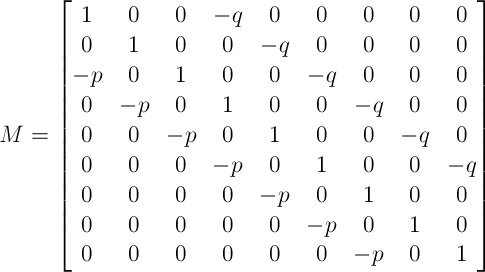
А если подставить значения:

А вектор C_j выглядел бы следующим образом:

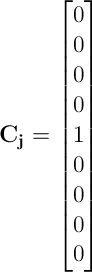
В то время как задача умножения матрицы/вектора весьма тривиальна, задача транспонирования матрицы больше 3×3 таковой не является. Простейший способ найти обратную матрицу M^-1 с помощью компьютера – LU-разложение. С помощью матрицы L можно решить уравнение Ly = I и найти y, а затем использовать матрицу U, чтобы решить уравнение Ux = y и найти x, которое и будет M^-1. После этого умножить три матрицы верхней части и три нижней части общей формулы вероятности разорения будет очень просто.

Оптимизация

Случай этого примера очень прост, матрица всего 9×9, обратную к ней матрицу можно рассчитать очень быстро безо всякой оптимизации. Но что, если НОД стратегии – $1? Например, если средние убытки $1 113, а средняя прибыль $1 109, то НОД составляет $1. При начальном остатке $2 500 и целевом остатке $5 000 это матрица 4,999×4,999, и для ее расчета потребуется много памяти компьютера и много времени. Лучшее время для расчета риск разорения без оптимизации – O(k^2.376), и, как правило, он требует не менее k×k памяти.

Во-первых, важно сохранить матрицу M^-1 по возможности небольшой. В идеале k должно быть меньше 500, если цель – решить эту проблему в разумное время (за несколько секунд).

Во-вторых, требуемую память можно существенно уменьшить: убыточный вектор можно сохранить внутри общего вектора (известно, где кончаются значения q в убыточном векторе и начинаются нули), а результаты LU-разложения можно сохранить внутри главной матрицы (M – она не будет удалена после разложения).

В-третьих, оба уравнения Ly = I и Ux = y можно решить для одного столбца (j-того), а не для всей матрицы k×k. Тот же самый столбец будет результатом и умножения на C_j. Это связано с тем, что, если вся матрица k×k рассчитывается и затем умножается на C_j, результат будет также просто j-м столбцом матрицы из-за всех нулей в C_j.

Наконец, можно рассчитать произведение убыточного вектора на j-ый столбец и одновременно произведение общего вектора на этот столбец, так как первые итерации убыточного шага будут во время расчета одинаковыми, а другие не потребуются в случае убыточного вектора.

Применение

Вот пример кода PHP, в котором вышеприведенный алгоритм используется для поиска риска разорения для более раннего примера:

/*
  Начальный остаток:      $2 500,00
  Целевой остаток:        $5 000,00
  Ср. убыточная сделка:     $1 500,00
  Ср. прибыльная сделка:   $1 000,00
  Вероятность понести убыток      30%
  Вероятность получения прибыли:       70%
*/

// Наибольший общий делитель= $500.
$begin_state = 5; // Начальный остаток, деленный на НОД.
$N = 9; // Количество переходных состояний; k в этой статье.
$loss_step = 3; // Размер убытков, деленный на НОД.
$loss_step = 2; // Размер прибыли, деленный на НОД.
$q = 0.3; // Вероятность понести убыток
$p = 0.7; // Вероятность получения прибыли.

// Заполняем вектор Cj.
for ($i = 0; $i < $N; $i++)
        if ($i == $begin_state - 1) $unitary_vector[$i] = 1;
        else $unitary_vector[$i] = 0;

// Заполняем убыточный вектор и общий вектор. Вообще-то убыточный вектор является частью общего вектора.
for ($i = 0; $i < $N; $i++)
        if (($i - $loss_step) < 0) $total_vector[$i] = $q;
        else if (($i + $win_step) >= $N) $total_vector[$i] = $p;
        else $total_vector[$i] = 0;

// Заполняем главную матрицу.
for ($i = 0; $i < $N; $i++)
        for ($j = 0; $j < $N; $j++)
                // Главная диагональ всегда 1.
                if ($i == $j) $a[$i][$j] = 1;
                // Элементы выше главной диагонали относятся к убыткам.
                if ($i == $j) $a[$i][$j] = 1;
                // Элементы ниже главной диагонали относятся к прибыли.
                else if ($j == $i - $win_step) $a[$i][$j] = -$p;
                else $a[$i][$j] = 0;

// LU-разложение.
for ($i = 0; $i < $N; $i++)
{
        for ($j = $i; $j < min($N, $i + $loss_step); $j++) // U
                for ($k = 0; $k <= $i - 1; $k++)
                        $a[$i][$j] -= $a[$i][$k] * $a[$k][$j];

        for ($j = $i + 1; $j <= min($i + $win_step, $N - 1); $j++) // L
        {
                for ($k = 0; $k <= $i - 1; $k++)
                        $a[$j][$i] -= $a[$j][$k] * $a[$k][$i];
                $a[$j][$i] /= $a[$i][$i];
        }
}

// Решение уравнения Ly = I для одного столбца (unitary_vector), который равен Cj из формулы разорения игрока.
// Итоговый у будет также сохранен в unitary_vector.
// Начинайте с begin_state, так как все иксы до 1 в unitary_vector всегда будут равны 0.
for ($i = $begin_state; $i < $N; $i++)
{
        $sum = 0;
        для ($j = 0; $j <= $i - 1; $j++)
                $sum -= $a[$i][$j] * $unitary_vector[$j];

        $unitary_vector[$i] = $unitary_vector[$i] + $sum;
}

// Решение уравнения Ux = y для одного столбца, рассчитанного в Ly = I.
// Итоговое значение x будет сохранено в unitary_vector.
for ($i = $N - 1; $i >= 0; $i--)
{
        $sum = 0;
        for ($j = $N - 1; $j > $i; $j--)
                $sum -= $a[$i][$j] * $unitary_vector[$j];

        $unitary_vector[$i] = ($unitary_vector[$i] + $sum) / $a[$i][$i];
}

// Умножение total_vector и его убыточной части на итоговый unitary_vector.
$loss = 0;
$total = 0;
for ($i = 0; $i < $N; $i++)
{
        $product = $total_vector[$i] * $unitary_vector[$i];
        if (($i - $loss_step) < 0) $loss += $product;
        $total += $product;
}
$probability = $loss / $total;
echo "Убыточный: $loss <br>";
echo "Общий: $total <br>";
echo "Вероятность: $probability <br>";

Результат на выходе будет:

Убыточный: 0,25755603952
Общий: 1
Вероятность: 0,25755603952

Таким образом, риск лишиться всего остатка на счете до его удвоения составляет в этом примере 25,8%.

Но что, если к станет слишком большим? В этом случае следует применить математическое округление к убыточному шагу, прибыльному шагу, а также к начальному и целевому остаткам путем практического отбрасывания нескольких последних цифр. Кроме того, можно уменьшить целевой остаток. Первый способ влияет на точность, но его эффект становится менее важным, так как разница между средним убытком и средней прибылью становится больше.

Преимущества

1. Если делается допущение, что входные данные (вероятности и размер прибыли/убытков) точны на 100%, то этот способ обеспечивает идеально точный результат.
2. Зависит не от способа определения размера позиции, а, скорее, от полученного в результате среднего убытка/прибыли в абсолютном выражении. Эта статистика имеется во всех отчетах о стратегиях на рынке Форекс.
3. Другие входные параметры тоже очень просты, и нет необходимости рассчитывать стандартное отклонение.
4. Простые случаи можно обсчитать вручную.
5. Рассчитанный риск "лишиться всего до достижения целевого остатка" – это что-то достижимое в отличие от "бесконечного количества сделок" предыдущих способов.

Недостатки

1. Делается допущение, что главные параметры торговой стратегии (размеры и соотношения прибыли/убытков) не меняются. В реальном мире так почти не бывает.
2. Это очень сложный метод.
3. Во многих случаях требуются значительные вычислительные возможности и много округления, снижающего точность.

Риск разорения в модели Монте-Карло

Имитационная модель Монте-Карло (также называемая методом Монте-Карло) – модель, предсказывающая вероятность различных исходов, когда присутствует вмешательство случайных величин. Изобретенная математиком Станиславом Уламом, она названа в честь Монте-Карло как популярного центра азартных игр в Монако. Название кажется очень подходящим, так как азартные игры обычно связаны с вероятностью и случайными результатами.

Суть метода Монте-Карло в том, чтобы имитировать результат много раз со случайными переменными и получать при каждой симуляции новые значения. Чтобы лучше понять, как работает этот метод, рассмотрим гипотетическую ситуацию.

Вы использовали исторические данные и бэктестинг и рассчитали вероятность понести убыток или получить прибыль от средней сделки при вашей торговой стратегии, а также средний размер прибыли и убытка. Как рассчитать риск разорения на основе этих данных? Можно попробовать имитировать результат путем рандомизации каждой сделки и выяснения того, сохранится ли в итоге остаток на вашему счету. Но одна симуляция мало полезна, поскольку показывает всего один результат из многих возможных и не объясняет, насколько он вероятен.

Но что, если имитировать этот результат сто раз? А тысячу? Или десять тысяч? Метод Монте-Карло предполагает, что путем рандомизации результата каждой сделки (прибыли или убытка и, возможно, размера прибыли или убытка) можно получить ценные статистические данные при повторном прогоне таких симуляций. И чем больше симуляций вы выполните, тем более надежными будут эти данные. В случае торговле на Форексе, посмотрев, сколько раз применение вашей стратегии привело к полному опустошению вашего счета, вы сможете определить риск разорения.

Пример симуляции Монте-Карло в таблице Excel

В этой таблице Excel показан пример простой симуляции Монте-Карло. Делается допущение, что вам известна вероятность того, что сделка будет прибыльной, а также размер средней прибыли и среднего убытка.

Введите размер остатка на вашем счете в поле "Начальный остаток на счете". Введите шанс получить прибыль в поле "Шанс получить прибыль" как число от 0 до 1. Например, если шанс получить прибыль составляет 65%, вы должны ввести 0,65. Далее введите среднюю прибыль и средний убыток в надлежащее поле. При желании использовать диапазон вместо фиксированной средней воспользуйтесь функцией RANDBETWEEN. После этого введите желательное число симулируемых сделок и количество симуляций, соответственно, в поле "Число сделок" и поле "Число симуляций". Заполнив все поля, вы сможете рассчитать риск разорения. Для этого зайдите в "Формулы" в главном меню Excel и нажмите "Рассчитать сейчас" справа от "Параметров вычислений". Или же просто нажмите на F9. Результат расчета появится в поле "Риск разорения" как процентный показатель

Под входными данными таблицы вы увидите строку с номерами сделок. Еще ниже будут строки с итоговыми остатками на счете при каждой сделке, и каждая строка будет представлять одну симуляцию.

Каждая сделка либо прибавляет сумму средней прибыли к остатку на счете, либо вычитает из него сумму среднего убытка в зависимости от того, ниже или выше случайное число, генерированное для этой сделки, значения шанса получить прибыль. Если при какой-то сделке остаток на счете становится нулевым или отрицательным, эта симуляция останавливается и считается "разоренной".

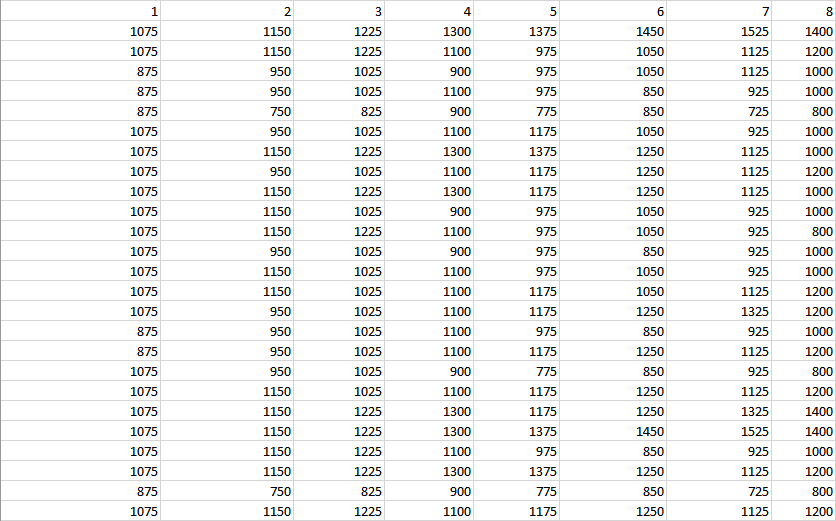
Если вы захотите иметь больше симуляций, чем лимит в 1 000 симуляций, допускаемый данной таблицей, вы можете легко скопировать и вставить строки ниже – формулы должны работать корректно. То же касается количества сделок на одну симуляцию. Можно скопировать и вставить столбцы после сделки № 1 000, чтобы увеличить максимальное количество сделок.

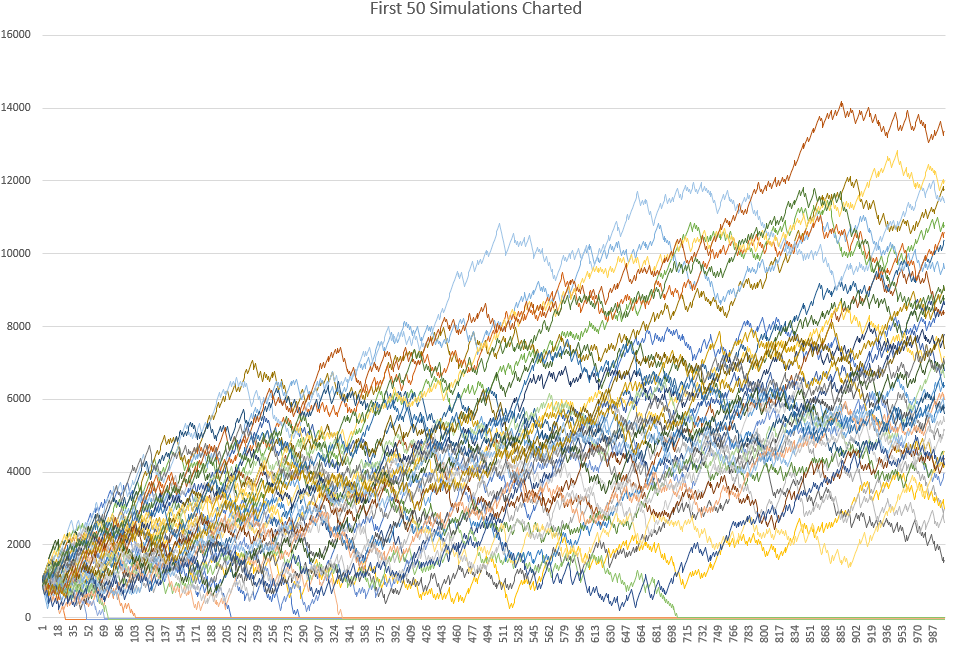
Вот график с наложенным примером первых 50 симуляций. Обратите внимание, что некоторые из них достигают нулевой линии и остаются на ней – это симуляции, в которых данная стратегия привела к опустошению счета.

Преимущества

1. Симуляция Монте-Карло – простое понятие, не требующее больших математических познаний.
2. Используя множество симуляций с меняющимися переменными, можно получить более точную вероятность разорения, чем при использовании простых средних значений.
3. В Интернете существует множество инструментов для выполнения симуляций Монте-Карло – от веб-страниц до расширений Excel.

Недостатки

1. Симуляция Монте-Карло делает допущение об "идеальном рынке", то есть не учитывает фундаментальные изменения, будь то краткосрочные изменения из-за важных событий (таких, как COVID-19) или долгосрочные изменения из-за структурных сдвигов в функционировании рынка (пример тому – "привязка" и последующая "отвязка" курса швейцарского франка от евро Швейцарским национальным банком). Такие изменения делают используемые для расчетов исторические данные бесполезными.
2. Изменение вашей торговой стратегии может тоже сделать ваши исторические данные неуместными, что означает, что симуляция Монте-Карло должна применяться только для тестирования постоянно применяемых торговых стратегий.
3. Симуляция Монте-Карло делает допущение о независимости каждой сделки от предыдущих. Поэтому она не подходит для скоординированных стратегий со сделками, учитывающими результаты предыдущих сделок.

Заключение

Ни один из описанных методов не идеален. Каждый из них должен применяться только при его соответствии параметрам стратегии торговли на Форексе:

• Формула фиксированного размера позиции хороша, когда вы знаете, что размер позиции фиксирован, можете рассчитать стандартное отклонение, а вклад убыточных позиций в стандартное отклонение больше, чем вклад изменчивости прибыльных позиций. Это хороший метод, если вы не хотите проводить никаких сложных расчетов.
• Формула определения фиксированного дробного размера позиции идеальна для стратегий определения дробного размера позиции. Опять-таки необходим поиск стандартного отклонения. Также необходим учет как прибыльных, так и убыточных позиций.
• Метод расчета риска разорения игрока™ рекомендуется, когда вы уверены, что статистические параметры торговой стратегии (средняя прибыль/убыток, соотношение прибыли и убытка) стабильны и вы не против того, чтобы провести действительно сложные расчеты.
• Метод Монте-Карло может быть полезен, когда у вас есть доступ к подходящему симулятору.

Какой бы способ вы ни выбрали, важно помнить, что не стоит воспринимать слишком всерьез само итоговое значение риска. Ведь его главная цель – сравнить различные стратегии или эффект от изменений, внесенных в одну торговую стратегию. Отношение к рассчитанному значению риска как к реальному показателю рискованности стратегии может привести к непредсказуемым и ужасным последствиям.

Если у вас возникнут какие-либо вопросы или комментарии по поводу оценки риска разорения при торговле на Форексе, обсудите их на нашем форуме.