每位外汇交易者都想知道他们交易策略的风险有多大，以及他们亏掉部分或全部本金的几率有多高。这种几率被称为破产风险。由于外汇交易者通常会知晓他们的盈/亏比率以及他们盈利或亏损头寸的平均数量，破产风险的计算应当是相对简单的。但确实如此吗？可惜事实并非如此。
破产风险是概率论中的一个已知问题，在某种程度上，它可以通过概率理论中的定律和公式来解决。评估外汇中的破产风险是一项非常复杂的任务，它需要大量的研究和计算能力，具体取决于（呈指数型）所需的评估准确度。
计算外汇策略破产风险最常用的方法有两种，即目前由许多外汇社交网站（例如 FXSTAT 和 Myfxbook 等）所采用的两种静态公式：固定头寸规模和固定分数头寸规模。公式由 D.R.Cox 和 H.D.Miller 在《The Theory of Stochastic Processes》（随机过程理论）一书中提出，并在各种来源渠道中公开可用（例如在 2009 年 8 月发布的《期货》杂志中的《Minimizing Your Risk of Ruin》（将破产风险最小化）一文，作者是 David E. Chamness）。一开始，它们可能看起来很复杂，但您可以通过计算器或 Excel 表格来计算它们。
用固定头寸规模来计算破产风险
固定头寸规模意味着外汇交易者不会随着新的盈利或亏损而增加或减少头寸规模。例如，如果交易者从 $10,000 的账户本金和每份头寸一标准手开始交易，无论本金下跌至 $1,000 还是上涨至 $50,000，这都不会改变一手头寸的交易量。亏损一部分本金的概率与账户的标准差成指数比例，与这部分本金数额和每笔交易的平均回报成反比。破产风险的公式如下所示：
其中：
- e 代表欧拉数 (~2.71828)，
- A 代表每笔交易的平均回报率（例如，如果您的头寸为账户带来 2% 的平均回报，则 A = 0.02），
- Z 代表账户余额的一部分，即您正在评估其风险的部分（例如，如要计算账户亏损 40% 本金的风险，Z = 0.4），
- D 代表交易回报的标准差（应该以相对形式，而不是货币单位计算）。
示例 1：
计算亏损 10% 本金的风险时，考虑到头寸的平均回报为 2%，标准差为 7%：
示例 2：
计算全部破产风险（亏损所有本金）时，考虑到头寸的平均回报为 1.5%，标准差为 1%：
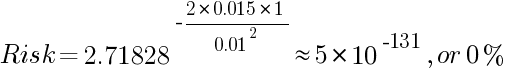
不难发现，这项公式计算的是无限量交易的风险。从公式可知，对于当前显示负交易预期的系统，亏损风险将始终为 100%，而且，如果平均收益足够高而回报标准差足够低，它将始终足够接近（但不等于）0。
优点：
- 这种方法很简单，公式本身可以通过计算器计算。标准差更难计算，但如果知道每笔交易后的账户余额，手动计算只需几分钟。只需一个简单的循环即可通过智能交易系统或其他脚本来完成计算。
- 计算结果非常精确。
- 它可以用于计算账户任意部分的亏损风险。
缺点：
- 它用标准差替代交易的实际“风险”，这并不是完全正确的。
- 它假设当前回报率和标准差不会随着时间改变。在实际交易中，固定不变的回报率和头寸规模几乎是不可能的。
- 它假设头寸规模为固定大小，但亏损掉一部分交易本金后，这可能会迫使外汇交易者减少头寸规模（例如，如果账户余额从 $10,000 下跌至 $800，则大概率无法使用一标准手的头寸规模）。
- 它显示无限量交易的风险，但没人会交易那么久。
- 即使所有假设对于给定的交易策略完全有效，准确性依然不能达到百分之百。
用固定分数头寸规模来计算破产风险
与固定头寸规模的模型不同，固定分数头寸规模意味着交易者在每笔交易中将固定比例的账户余额投入风险（例如 1%；这个实际值在这里并不重要），因此，利润与账户规模成正比，亏损与账户规模成反比。与固定头寸规模一样，亏损部分本金的概率依然与这部分本金数额成指数性反比。风险依然与标准差成正比，与本金部分数额成反比，但它的性质更加复杂。风险计算公式如下所示：
其中：
- e 代表欧拉数 (~2.71828)，
- A 代表每笔交易的平均回报率（例如，如果头寸为账户带来 14% 的平均回报，则 A = 0.14），
- Z 代表账户余额的一部分，即您正在评估其风险的部分（例如，如要计算账户亏损 25% 本金的风险，Z = 0.25），
- D 代表交易者回报的标准差（应该以相对形式，而不是货币单位计算）。
- ln 代表自然对数。
以下是使用固定分数头寸规模模型来计算破产风险的两个示例，条件与上文中固定头寸规模示例的条件相同：
示例 1：
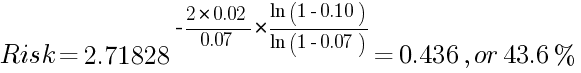
显然，它只比固定头寸规模模型的 44.2% 略低一点。
示例 2：
由于如果公式计算 100% 的账户余额，这意味着 Z = 1，则自然对数的计算会出现错误（未定义 0 的自然对数，但它是一个无限大的负数）这意味着，如果策略拥有正回报率并且采用固定比例的头寸规模，则不可能会亏掉所有本金：
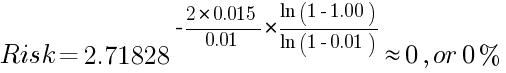
显然，这项公式显示的风险更低，因为它考虑的是一部分头寸，可以减少亏损的头寸数量，从而进一步减少亏损。
优点：
- 这种用于评估破产风险的方法依然很简单。与固定头寸规模公式相比，这种方法只添加了几个新步骤，但采用的数据相同。
- 这种头寸规模模型的结果更精确。
- 它可以用于计算账户任意部分的亏损风险。
缺点：
- 与固定头寸规模公式相同，它的实际风险被替换为标准差。
- 假设回报率和标准差固定不变。
- 它计算的是无限量交易的风险。
使用马尔可夫（Markov ）链来计算赌徒破产问题
就所涉及的实际计算而言，计算亏损风险最直观的方法其实也是最难的方法。外汇破产风险可以被定义为一种特定类型的赌徒破产问题，其中，交易者（玩家）投入一笔初始本金，他有一定的概率来赢得特定平均盈利，也有一定的概率会出现特定平均亏损，这两个概率可能不同，也可能相同。交易者的竞争对手是市场（这是一个无限富有的对手）），因此，只有交易者才能让账户破产；盈利条件可以被定义为达到某个高于起始本金的目标余额。
如要了解更多关于使用此方法来计算亏损风险的简单公式的背景研究，请参考 Charles M. Grinstead 和 J. Laurie Snell 的《Introduction to Probability》（概率导论）一书的第 12 章。
盈利与亏损相等，概率相同
如果平均盈利等于平均亏损，而且亏损概率等于盈利概率，那么破产风险的计算相当简单。起始本金用 z 表示，目标余额用 M 表示。账户余额从 z 变为 M 的破产风险为：
示例 1：
起始本金为 $10,000（z）。每笔交易盈利或亏损 $1,000 的概率为 50/50。目标余额为 $20,000（M）。
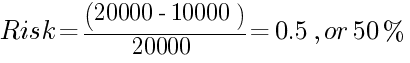
显然，本示例中本金从 $10,000 盈利至 $20,000 或亏损至 $0 的概率相同。
盈利与亏损相等，概率不同
盈利概率（p）- 是指是赢得（最终获取利润）一份头寸的几率。如果交易者能知道他们赢得特定交易的确切概率，那会很有意义，但此处将使用盈/亏比率。盈利概率的计算方式是用盈利交易的数量除以总交易数。此处可以包含
亏损概率（q）- 是指亏掉（以亏损结束）一份头寸的几率。与上述原因相同，简单的盈/亏比是可用于此处的最佳估计值。q = 亏损交易数 / 总交易数。显然，虽然计算 p 时会计入零盈利头寸，但此处不应将它们包含在内。
如果某笔特定交易的盈利概率与亏损概率不同，则采用的公式会略微复杂一些。赢得一笔平均盈利交易的概率为 p，亏损一笔交易的概率为 q（p + q = 1）。破产风险的计算方式如下所示：
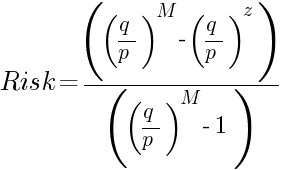
示例 2：
同样，起始本金为 $10,000（z），目标余额为 $20,000（M），每笔交易的平均盈/亏为 $1,000，但本例中的盈利概率为 0.55，亏损概率为 0.45（交易系统拥有 5% 的优势）。为了简化计算过程，可将起始本金和目标余额都除以平均盈/亏比，得到 z = 10，M = 20。余额翻倍前，破产风险的计算方法如下：
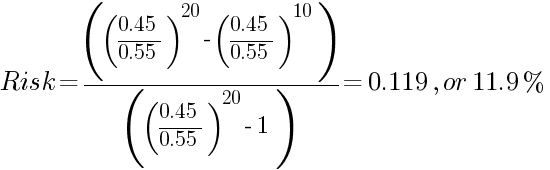
显然，5% 的优势使外汇交易者整个交易系统的可靠性有了巨大的提升。
盈利与亏损不同，概率不同
实际上，外汇交易策略很少会以平均盈利等于平均亏损的形式运行。盈利和亏损头寸结果的不同会导致破产风险的计算方式也有很大的不同。在本例中，并没有必要详细列出完整的计算算法。相反，最好是提供必要步骤的综述，而且这些步骤可以轻松简化为简单的数学/代码问题。
数学计算
有关一般情况下破产风险计算的详细信息（盈利与亏损不同，概率不同）可以在 Kevin Brown 的文章《The Gambler's Ruin》中找到。这篇文章很好地解释了这个问题和相关的解决办法。
交易过程可以表示为一个
通常，账户在达到目标余额前亏掉所有本金的概率计算公式如下所示：
![风险 = ([q...(q)(0...0)(0)...0]M^-1Cj)/([q...(q)(0...0)(p)...p]M^-1Cj)](/img/articles/blog/2011/10/gamblers-ruin-general-case-matrix-risk-of-ruin.png "风险 = ([q...(q)(0...0)(0)...0]M^-1Cj)/([q...(q)(0...0)(p)...p]M^-1Cj)")
其中：
- p 指交易盈利的概率。
- q 指交易亏损的概率。
- 上部
行向量 （亏损向量）的长度为 k。首个平均亏损/GCD (亏损步长) 的元素为 q，其他为 0。 - 下部
行向量 （总向量）的长度也为 k。首个平均亏损/GCD（亏损步长）元素为 q，最后一个平均盈利/GCD（盈利步长）元素为 p, 其他为 0。 - M-1 是系数矩阵 M 的逆矩阵。M 是一个 k×k 矩阵，它所有的主对角元素均包含 1。除了对角元素 1，每一列均最多包含两个
非零 元素：-P - 位于主对角线下方，其垂直偏移等于盈利步长； -q - 位于主对角线上方，其垂直偏移等于亏损步长。 - Cj 指
大小为 k 的单列矩阵（向量），其中除了位置 j（起始状态）处的元素等于 1，其他所有元素均为 0。
在上述示例中，矩阵 M 如下所示：
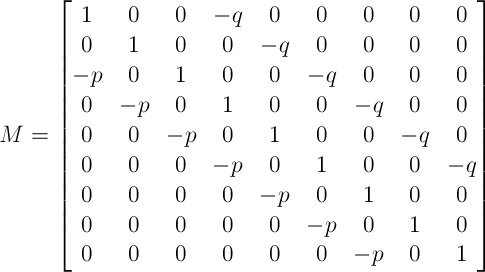
赋值后：
向量 Cj 将如下所示：
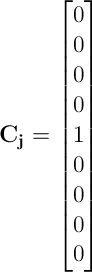
虽然矩阵/向量乘法很简单，但如果矩阵大于 3×3，则矩阵求逆并不轻松。
优化
示例非常简单，矩阵仅为 9×9，可以轻松求逆且无需进行任何优化。但如果交易策略的 GCD 是 $1 呢？例如，如果平均亏损为 $1,113，平均盈利为 $1,109，则 GCD 为 $1。如果起始本金为 $2,500，目标余额为 $5,000，即矩阵为 4,999×4,999，
首先，应当使 M-1 矩阵尽可能小。如果交易者的目标是要在合理时间内（几秒钟）解决这个问题，k 应当小于 500。
其次，应尽量减少所需的内存：亏损向量可以存储在总向量中（已知 q 在亏损向量结束和 0 向量开始时），还可以将 LU 分解的结果存储在主矩阵（M - 分解后可不再使用）中。
另外，Ly = I 和 Ux = y 可以只求解一列（第 j 列），而不是整个 k×k 矩阵。同一列也是与 Cj 相乘的结果。因为如果计算整个 k×k 矩阵并乘以 Cj, 由于 Cj 中的所有零值，得出的也是矩阵第 j 列的结果。
最后，可以同时计算亏损向量与第 j 列的乘积以及总向量与该列的乘积，因为在相关计算过程中，第一个亏损步长的迭代是相同的，而亏损向量无需计算其他迭代。
执行
以下是使用上述算法来查找前文中破产风险的 PHP 代码示例：
/* 起始本金： $2,500.00 目标余额： $5,000.00 平均亏损交易： $1,500.00 平均盈利交易： $1,000.00 亏损概率： 30% 盈利概率： 70% */ // 最大公约数 = $500。 $begin_state = 5; // 起始本金除以 GCD。 $N = 9; // 过渡状态的数量；本文中为 k。 $loss_step = 3; // 亏损数额除以 GCD。 $win_step = 2; // 盈利数额除以 GCD。 $q = 0.3; // 亏损概率。 $p = 0.7; // 盈利概率。 // 填充 Cj 向量。 for ($i = 0; $i < $N; $i++) if ($i == $begin_state - 1) $unitary_vector[$i] = 1; else $unitary_vector[$i] = 0; // 填充亏损向量和总向量。亏损向量实际上是总向量的一部分。 for ($i = 0; $i < $N; $i++) if (($i - $loss_step) < 0) $total_vector[$i] = $q; else if (($i + $win_step) >= $N) $total_vector[$i] = $p; else $total_vector[$i] = 0; // 填充主矩阵。 for ($i = 0; $i < $N; $i++) for ($j = 0; $j < $N; $j++) // 主对角线始终为 1。 if ($i == $j) $a[$i][$j] = 1; // 主对角线上方的元素为亏损。 else if ($j == $i + $loss_step) $a[$i][$j] = -$q; // 主对角线下方的元素为盈利。 else if ($j == $i - $win_step) $a[$i][$j] = -$p; else $a[$i][$j] = 0; // LU 分解。 for ($i = 0; $i < $N; $i++) { for ($j = $i; $j < min($N, $i + $loss_step); $j++) // U for ($k = 0; $k <= $i - 1; $k++) $a[$i][$j] -= $a[$i][$k] * $a[$k][$j]; for ($j = $i + 1; $j <= min($i + $win_step, $N - 1); $j++) // L { for ($k = 0; $k <= $i - 1; $k++) $a[$j][$i] -= $a[$j][$k] * $a[$k][$i]; $a[$j][$i] /= $a[$i][$i]; } } // 对一列求解 Ly = I（unitary_vector），等于赌徒破产风险公式的 Cj。 // 得出的 y 也会存储在 unitary_vector 中。 // 从 begin_state 开始，因为 unitary_vector 中 1 之前所有的 X 将始终为 0。 for ($i = $begin_state; $i < $N; $i++) { $sum = 0; for ($j = 0; $j <= $i - 1; $j++) $sum -= $a[$i][$j] * $unitary_vector[$j]; $unitary_vector[$i] = $unitary_vector[$i] + $sum; } // 对一列求解 Ux = y，在 Ly = I 中计算。 // 得出的 x 将储存在 unitary_vector 中。 for ($i = $N - 1; $i >= 0; $i--) { $sum = 0; for ($j = $N - 1; $j > $i; $j--) $sum -= $a[$i][$j] * $unitary_vector[$j]; $unitary_vector[$i] = ($unitary_vector[$i] + $sum) / $a[$i][$i]; } // 将 total_vector 及其亏损部分与得出的 unitary_vector 相乘。 $loss = 0; $total = 0; for ($i = 0; $i < $N; $i++) { $product = $total_vector[$i] * $unitary_vector[$i]; if (($i - $loss_step) < 0) $loss += $product; $total += $product; } $probability = $loss / $total; echo "Loss: $loss <br>"; echo "Total: $total <br>"; echo "Probability: $probability <br>";
输出结果为：
亏损：0.25755603952 总值：1 概率：0.25755603952
因此，在本示例中，账户在余额翻倍前亏掉全部本金的风险约为 25.8%。
但如果 k 的数值太大呢？在这种情况下，亏损步长、盈利步长以及起始和目标余额将进行数学取整，这实际上会截掉最后几个数字。此外，这样可能会减少目标余额。第一种方法会影响准确性，但随着平均亏损和平均盈利之间的差异拉大，这种影响会逐渐变小。
优点
- 假设输入数据（概率及盈/亏数额）是 100% 准确的，那么这种方法会给出非常准确的结果。
- 它并不取决于头寸规模方法，而是取决于以绝对数值显示的平均亏损/盈利，这些数值是所有外汇策略报告中随时可用的统计数据。
- 其他输入参数也很简单，无需计算标准差。
- 如果案例简单，可手动计算。
- 计算出的风险是“在达到目标余额之前亏掉所有本金”的风险。与前文方法中的“无限量交易”相反，这种风险是有可能实际发生的。
缺点
- 它假设交易策略的主要参数（盈/亏数额及比率）不会变化。实际上，这几乎不太可能。
- 这种方法很复杂。
- 在许多情况下，它需要大量计算能力或大量取整，因而有可能会降低结果的准确性。
用蒙特卡洛（Monte Carlo）模拟法计算破产风险
蒙特卡洛模拟（也被称为蒙特卡洛方法）是一种可预测涉及随机变量的不同结果概率的模型。它的发明者是数学家 Stanislaw Ulam，并以摩纳哥著名的赌博胜地蒙特卡洛命名。这个名字取得很恰当，因为赌博经常与机会和随机结果挂钩。
蒙特卡洛方法的基本要点是多次模拟结果，让随机变量在每次模拟中获得新值。为了更好地了解这种方法的原理，我们来关注一种假设情境。
通过历史数据和回测，您可以针对您的交易策略计算交易平均亏损或收益的几率，以及收益或亏损的平均数额。那么，如何使用这项数据来计算破产风险呢？您可以尝试通过随机设置每笔交易来模拟结果，并查看您的账户余额最后是否会清零。但如果只进行一次模拟，则它的用处不大，因为它只显示许多可能性中的一种结果，而且这种结果不一定是真实的。
但如果您模拟一百次呢？或者一千次？一万次？蒙特卡洛方法说明，通过随机获得每笔交易的结果（收益或亏损，以及收益或亏损的数额），您可以在重新运行此类模拟时获得有价值的统计数据。而且，您模拟的次数越多，获得的数据就越可靠。在外汇交易中，您可以观察交易策略导致您账户本金归零的次数，并以此来确定破产风险。
Excel 表格中的蒙特卡洛模拟示例
Excel 表格显示了一个简单的蒙特卡洛模拟示例。它假设您已知盈利交易的概率以及平均收益和平均亏损的数额。
在启动账户余额字段中输入您的账户余额大小。在盈利几率字段中输入介于 0 至 1 之间的数。例如，如果收益几率为 65%，您应该输入 0.65。下一步，在合适的字段中输入平均收益和平均亏损。如果您想使用区间，而不是固定平均值，您可以通过RANDBETWEEN（随机整数）函数轻松实现。之后，分别在 # of Trades 和 # of Simulations 字段输入所需的模拟交易数量及模拟次数。填写完所有字段后，您可以计算破产风险。为此，请前往 Excel 主菜单中的“公式”，然后点击“计算选项”右侧的“立即计算”。另外，您也可以只点击
重要事项！ 计算可能会花费较长的时间，尤其是在运行速度缓慢的电脑上，而且电子表格上的任意点击都可能会打断计算，进而产生错误的结果。计算开始后，最好不要与电子表格进行交互操作，直到屏幕左下角显示“就绪”字样。
在表格的输入栏下方，您会看到一行交易数值。再下方是每笔交易的账户余额，每一行代表一次模拟。
每笔交易会从账户中增加平均收益金额或减去平均亏损金额，具体取决于该笔交易生成的随机数值是低于还是高于盈利几率值。如果某笔交易后，账户余额变为零或负值，则模拟将会结束并被视为“破产”。
如果您想让指定的电子表格进行多达 1,000 次的模拟，您可以轻松地将行数据复制到更远的位置——公式应该可以正常运行。与每次可模拟的交易数量相同，您可以将列复制和粘贴至 #1,000 交易之后，以增加最大交易数量。
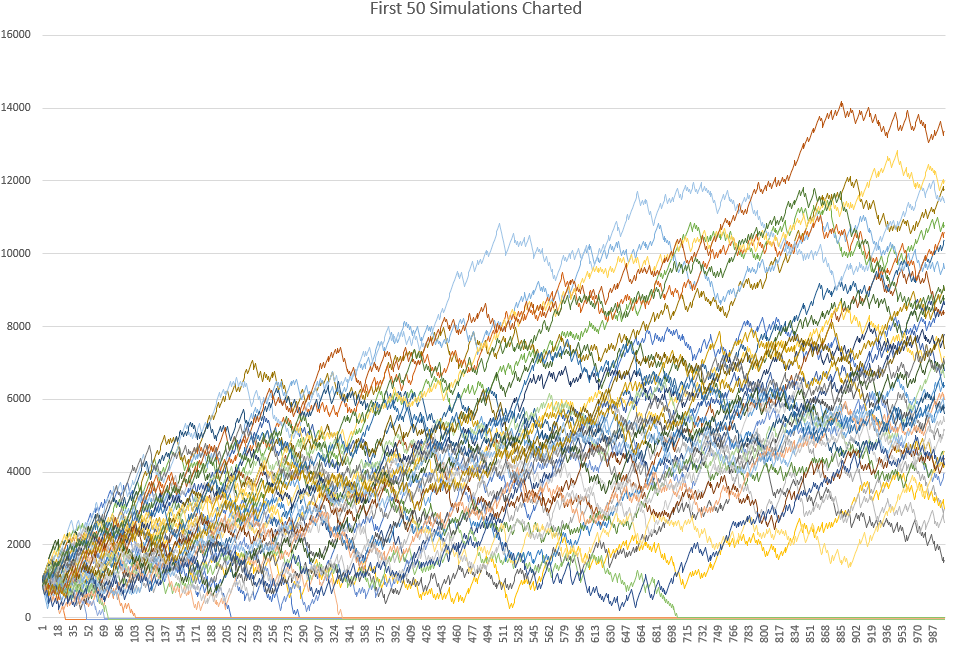
以下是绘制了前 50 次模拟的示例图表。请注意，有些模拟到达零线后保持不变，代表在这些模拟中，交易策略导致交易账户破产：
优点
- 蒙特卡洛模拟是一项简单的概念，不涉及复杂的数学计算。
- 通过用可变变量进行多次模拟，您可以计算出比单纯使用简单平均值更准确的几率。
- 网上有许多可进行蒙特卡洛模拟的工具，包括网页和 Excel 插件等。
缺点
- 蒙特卡洛假设“市场是完美的”，意味着它不考虑基本面变化，无论这种变化是由于重要事件（例如新冠疫情）引起的短期变化，还是由于市场运作方式发生结构变化而引起的长期变化（例如瑞士国家银行将瑞士法郎与欧元“挂钩”后又“脱钩”）。此类变化会导致用于计算的历史数据失去作用。
- 改变交易策略也会导致历史数据失去关联，这说明蒙特卡洛模拟只应用于经过一致性测试的交易策略。
- 蒙特卡洛模拟假设每笔交易均独立于之前的交易。因此，它不适合那些需将历史交易结果纳入交易考量范围的序列相关策略。
结语
上文中的方法都不完美。每一种都只适用于与外汇交易策略参数相符的情况：
- 固定头寸规模公式适用于以下情况：您知道头寸规模是固定的，您可以计算标准差，以及标准差中亏损头寸的输入范围大于盈利头寸的可变范围。如果您不想进行任何复杂的计算，它不失为一种好方法。
- 固定分数头寸规模公式适合那些采用一定比例头寸规模的策略。同样，寻找标准差是很有必要的。它也应当由亏损头寸和盈利头寸组成。
- 赌徒破产法适用于当您确信交易系统的统计参数稳定不变且您愿意做一些非常复杂的计算时。
无论您采用哪种方法，请务必要记住，不应过于看重由这些方法得出的风险值。它的主要目的是对比不同的交易策略或应用于某项交易策略的变化效果。如果将计算出的风险值作为衡量策略风险的真正标准，这可能会导致意料之外但又非常可怕的后果。
注意： 通过外汇报告分析工具可以计算三种类型的破产风险。或许，这也是唯一提供此类功能的免费在线工具。
如果您有任何关于外汇交易破产风险评估的问题或意见，您随时可以免费到我们的论坛上探讨。
